Равновесие фаз при искривленной поверхности раздела. Капиллярность

На практике нередко приходится иметь дело сискривленной поверхностью раздела. Например, поверхность капли выпукла, а поверхность жидкости в смачиваемом капилляре вогнута.

Понятно, что молекула жидкости, находящаяся на выпуклой поверхности, будет испытывать равнодействующую силу, направленную в глубь жидкости, меньшую, чем на плоской поверхности. На вогнутой поверхности, наоборот, эта сила больше. Поэтому, если на плоской поверхности давление в обеих сосуществующих фазах одинаково, то на искривленной поверхности в условиях равновесия возникает добавочное давление, направленное в сторону той фазы, по отношению к которой поверхность вогнута. Другими словами, при равновесии давление в фазе, отделенной от другой фазы вогнутой поверхности, больше. Эта разность давлений, возникающая по обе стороны искривленной поверхности жидкости, носит название капиллярного (или лапласова) давления.

Величина капиллярного давления зависит от кривизны поверхности и поверхностного натяжения и выражается уравнением Лапласа.

Рассмотрим элементарный участок искривленной поверхности с площадью

S = l1 × l2.                                                                                                                                  (12.6)

Если r1 и r2 – радиусы кривизны криволинейных отрезков l1 и l2, то площадь S равна

S = l1 × l2 = r1 j1× r2j2,                                                                                                              (12.7)

где j1 и j2 – соответствующие центральные углы (рис. 12.1).

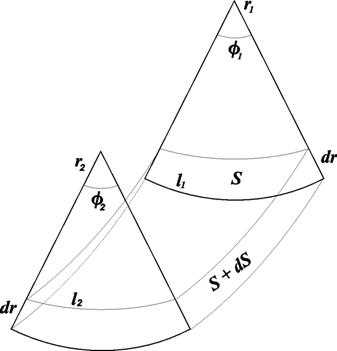
Рис. 12.1. Элементарный участок искривленной поверхности

Если под действием, вызванным разностью давлений DР по обе стороны поверхности, сама поверхность сместилась на величину dr без изменения кривизны, то произошло увеличение этой поверхности на величину dS. Затраченная работа dW может быть вычислена двумя способами: работа dW равна произведению силы на путь:

dW = DРSdr,                                                                                                                           (12.8)

но эта же работа dW равна произведению поверхностного натяжения на прирост поверхности:

dW = s×dS.                                                                                                                             (12.9)

Поэтому

s×dS = DРSdr = j1j2r1 r2DРdr.                                                                                              (12.10)

Найдем dS:

dS = j1j2 (r1 +dr)( r2 +dr) - j1j2r1 r2.                                                                                     (12.11)

После несложных преобразований, пренебрегая членом (dr)2 как величиной бесконечно малой второго порядка, получим:

dS = j1j2r1 dr - j1j2 r2dr.                                                                                                      (12.12)

Подставим уравнение (12.12) в уравнение (12.11) и разделим обе части уравнения на r1 r2j1j2 , получим формулу Лапласа, выражающую избыток давления со стороны вогнутой поверхности:

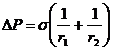.                                                                                                          (12.13)

Если поверхность сферическая, то r1 = r2 и лапласово давление равно

.                                                                                                                           (12.14)

Вследствие существования лапласова давления величина давления насыщенного пара жидкости при данной температуре зависит от формы поверхности.