Первое теоретическое уравнение изотермы адсорбции было предложено И. Ленгмюром в 1914 году. Теория Ленгмюра основана на трех основных положениях:
Адсорбция происходит на дискретных адсорбционных центрах, которые могут иметь различную природу.
При адсорбции соблюдается строгое стехиометрическое условие – на одном центре адсорбируется одна молекула.
Адсорбционные центры энергетически однородны и независимы, т.е. адсорбция на одном центре не влияет на адсорбцию на других центрах.
На основании этих положений скорость адсорбции Vaдc пропорциональна давлению газа и числу свободных центров. Если общее число центров аm, то при адсорбции, равной а, число свободных центров равно (аm – а).
Поэтому
Vaдc = kaдc × P × (am – a). (13.22)
Наряду с адсорбцией идет процесс десорбции:
Vдес. = kдес. × а. (13.23)
При равновесии Vaдc = Vдес или
kaдc × P × (am – a) = kдес. × а. (13.24)
Обозначим kдес./ kадс. = b, а а/аm = Q, где Q – относительное заполнение поверхности, получим:
![]() или
или ![]() . (13.25)
. (13.25)
Это уравнение изотермы адсорбции называется уравнением Ленгмюра. Константа b носит название константы адсорбционного равновесия, или адсорбционного коэффициента.
Константа равновесия связана со стандартными изменениями энергии Гиббса. Если
RTlnb = –DGo, так как DGo = DHo + TDSo,
то
![]() . (13.26)
. (13.26)
Следовательно
![]() . (13.27)
. (13.27)
Таким образом, адсорбционный коэффициент b связан со стантартной энтропией DS° и со стандартной теплотой адсорбции q = –DH°.
Очень часто аm называют «емкость монослоя». На рис.13.3 показана кривая, выражающая изотерму адсорбции по Ленгмюру
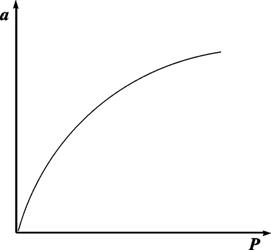
Рис. 13.3. Изотерма адсорбции по Ленгмюру
При очень малых заполнениях и, следовательно, очень малых давлениях Р в знаменателе, согласно (13.25), bр<< 1. Поэтому в этой области а = аmbp, т.е. переходит в уравнение Генри. При очень высоких давлениях bp >> 1 и а = аm, т.е. величина адсорбции перестает зависеть от давления, поскольку все центры уже заняты.
Для расчета параметров am и b уравнение Ленгмюра представляют в виде
![]() . (13.28)
. (13.28)
Тангенс угла наклона этой линии равен 1/amb, а отрезок, отсекаемый на оси ординат, равен 1/am.
Уравнение Ленгмюра, полученное на основании модели локализованной адсорбции газов на поверхности твердого тела, часто хорошо описывает адсорбцию растворенных веществ на поверхности жидкости (поверхность раздела раствор/газ), при которой адсорбция не локализована, так как молекулы подвижны и образуют двумерную газо- или жидкообразную пленку.
Обусловлено это тем, что основные положения модели Ленгмюра соблюдаются при адсорбции из растворов: поверхность жидкости идеально однородна, взаимодействие адсорбированных молекул в адсорбционном слое мало отличается от их взаимодействия в растворе. Оно к тому же ослаблено за счет взаимодействия молекул растворенного вещества с молекулами растворителя и практически не влияет на адсорбцию.
Уравнение Ленгмюра связано с уравнением состояния адсорбционной пленки – уравнением Гиббса. Так,
![]() ,
,
а по уравнению Ленгмюра
![]() ;
;
тогда
![]()
или
![]() . (13.29)
. (13.29)
После интегрирования в пределах от sо до s и от 0 до С получим:
![]() ,
,
и, наконец,
![]() , (13.30)
, (13.30)
где Г¥ связано с площадью, занимаемой 1 моль адсорбированного вещества в мономолекулярном слое, следующим соотношением: ![]() .
.
Поможем написать любую работу на аналогичную тему

