Для решения задачи, поставленной в предыдущем разделе, нужно задать период времени в годах (
), за который будет решаться задача. Этот период не должен быть больше морального износа (старения) технологического оборудования (≤
). Определение периода морального старения может относиться как к оборудованию, так и технологическому процессу в целом. Не исключено влияние на период морального старения технологического процесса и морального старения продукции, то есть повышение её технического уровня и качества изготовления.
Как отмечалось в предыдущем разделе, прежде всего, следует учитывать, что развитие технических характеристик продукции, технологии, оборудования и др. за период их жизненного цикла осуществляется по 
-образной кривой (рис.1.2.1).
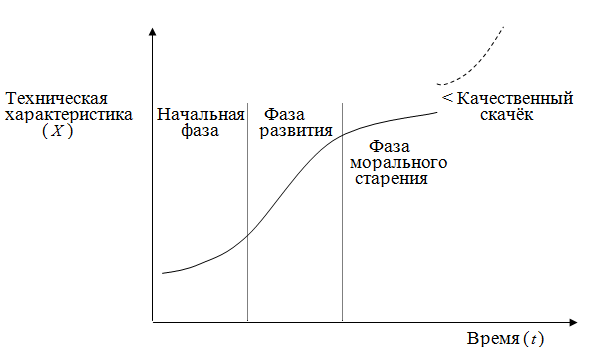
Рис. 1.2.1. Закономерность развития этапов жизненного цикла техники
Данная закономерность сходна с закономерностью развития этапов жизненного цикла товаров на рынке (из учебной дисциплины по маркетингу). Отличие в том, что жизненный цикл товара на рынке заканчивается с окончанием выпуска и реализации конкретного ассортимента (модификации) продукции. В то же время продукция (товар) у потребителя продолжает использоваться (эксплуатироваться) до окончания её технического или экономически целесообразного срока службы и утилизации.
Необходимость учёта данной закономерности при прогнозировании направлений улучшения качества продукции, развития производства и систем управления на предприятии заключается в том, что технические, организационные и другие инновации должны находиться в фазе своего развития, а не в фазе морального старения.
Следует также отметить, что учёт данной закономерности при прогнозировании является условием необходимым, но недостаточным. Анализ развития технических характеристик по конкретному виду техники за длительный период времени показывает, что S-образная закономерность повторяется (рис. 1.2.2., локальные кривые).
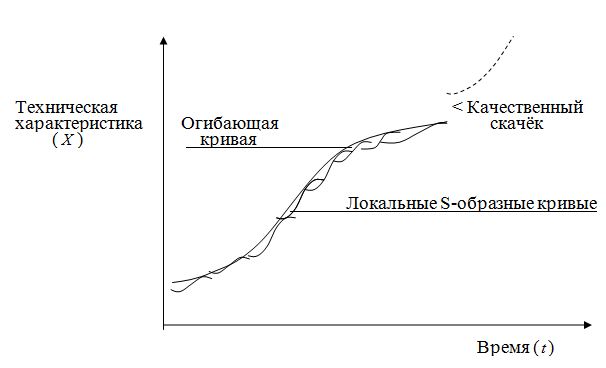
Рис. 1.2.2. Закономерность развития производства конкретной техники
за длительный период времени.
Огибающая (интегральная) кривая также имеет -образную закономерность. Поэтому нужно учитывать, что локальная кривая может находиться в фазе морального старения на огибающей кривой. В этом случае не будет иметь значение, в какой фазе на локальной кривой находится развитие той или иной инновации, нужно искать более прогрессивную инновацию.
Анализ выше изложенной закономерности в конкретной отрасли промышленности должен позволить предприятию определить место технического уровня технологии, оборудования и продукции в тенденциях научно-технического прогресса соответствующей отрасли. В результате анализа и будет определён период времени в годах (), за который будет решаться задача по экономическому обоснованию модернизации или замене оборудования конкретного технологического процесса.
Следующей подготовительной организационно-технической задачей будет выбор целей и направлений развития производства, в частности, направлений модернизации или замены оборудования конкретного технологического процесса.
Рассмотрим пример оценки целей (подцелей) и выбор направлений развития производства с использованием программного (нормативного) метода прогнозирования на графах. Данный метод можно использовать для решения и других задач прогнозирования, включая направления улучшения качества продукции, развития систем управления на предприятии и др.
Для постановки задачи нужно логическим или логистическим путём построить дерево целей. Возьмем упрощённый пример дерева целей с одной главной целью (рис. 1.2.3.). На практике их может быть несколько.
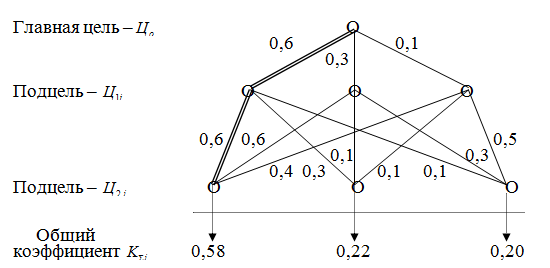
Рис. 1.2.3. Дерево целей
Содержание главной цели определяется по результатам анализа хозяйственной деятельности предприятия. В данном примере главная цель будет носить общий характер – развитие производства (
).
Для достижения главной цели определяются подцели на разных уровнях. Упрощая пример, возьмем два уровня. На первом уровне будут подцели (
) технического характера как возможные варианты:
1) модернизация оборудования;
2) замена технологии;
3) реконструкция предприятия, здесь возможно и перепрофилирование предприятия, и др.
4) Количество подцелей на первом уровне – 
(
).
5) На втором уровне будут подцели (
) экономического характера как возможные варианты (источники финансирования):
6) собственные средства;
7) кредиты;
8) организация акционерного общества (АО) (или совместного предприятия СП) и др.
Количество подцелей на втором уровне – 
(
).
Количество уровней может быть любым.
На каждом уровне для оценки значимости подцелей отбираются эксперты – специалисты в проблемах данного уровня. Как правило, участвует и руководство предприятия.
В нашем примере эксперты, специалисты в области техники, дали следующую оценку значимости подцелей первого уровня (табл. 1.2.1.).
Таблица 1.2.1
Подцели уровня главной цели 
|
№ п/п |
Подцели уровня |
Весовой коэффициент − |
|
1 |
Модернизация оборудования – |
0,6 |
|
2 |
Замена технологии – |
0,3 |
|
3 |
Реконструкция предприятия – |
0,1 |
|
i |
--------------------------------------------------------- |
|
|
|
1 |
|
Оценка подцелей второго уровня осуществляется другой группой экспертов, специалистов в области экономики. Эксперты дали следующую оценку подцелям второго уровня (табл. 1.2.2).
Таблица 1.2.2
Подцели уровня подцели .
|
№ п/п |
Подели уровня Ц2j (источники финансирования) |
Весовые коэффициенты – |
Общий коэффициент – |
|||
|
( |
( |
( |
||||
|
1 |
Собственные средства |
0,6 |
0,6 |
0,4 |
0,58 |
|
|
2 |
Кредит |
0,3 |
0,1 |
0,1 |
0,22 |
|
|
3 |
Организация АО или СП |
0,1 |
0,3 |
0,5 |
0,20 |
|
|
j |
------------------------ |
|
|
|
|
|
|
|
1 |
1 |
1 |
|
||
=0,6)
=0,3)
=0,1)
Общий коэффициент оценки подцелей второго уровня (
) с учётом значимости подцелей первого уровня определяется последующей формуле:
(1.2.1)
Поэтому общие коэффициенты оценки подцелей второго уровня будут иметь следующие значения:
=0,6·0,6+0,3·0,6+0,1·0,4=0,58;
=0,6·0,3+0,3·0,1+0,1·0,1=0,22;
=0,6·0,1+0,3·0,3+0,1·0,5=0,20.
Максимальные значение коэффициентов оценки значимости подцелей по уровням снизу вверх, то есть прогнозирование от будущего к настоящему, покажут целесообразные подцели развития производства. Тем самым, определится и направление (на рисунке 1.2.3 это путь, выделенный двумя линиями) достижения главной цели развития производства.
Для выбора направлений развития производства, включая технологические процессы и их оборудование, можно использовать метод экспертных оценок.
Во-первых, в предыдущем примере отмечалось, что оценка подцелей каждого уровня осуществляется самостоятельной группой экспертов. Определение репрезентативной группы экспертов по каждому уровню уже является самостоятельной задачей.
Во-вторых, возможна ситуация, когда затруднительно или нет необходимости строить дерево целей. В этом случае мы имеем цели приблизительно одного уровня. Оценка и выбор цели и будет являться задачей выбора направления улучшения качества продукции, развития производства и систем управления на предприятии и тд.
1. Прежде всего, как отмечалось выше, возникает задача определения репрезентативной группы экспертов. Для этого нужно оценить компетентность каждого эксперта.
Отметим один раз, чтобы не возвращаться к этому вопросу, что оценка экспертов и направлений развития предприятия осуществляется в баллах по соответствующей шкале. На практике, в зависимости от постановки задачи, используются следующие интервальные шкалы: или 0–1, или 0–10, или 0–100.
Компетентность каждого эксперта определяется по степени его осведомлённости об объекте прогнозирования на основе самооценки и оценки по анкетным данным.
В анкете самооценки (табл. 1.2.3) эксперт по своему усмотрению зачёркивает (отмечает) соответствующий балл (ячейку) в зависимости от степени его осведомлённости об объекте прогнозирования (о решаемой проблеме). Это будет учитываться в дальнейшем при определении компетенции эксперта.
Таблица 1.2.3
Анкета самооценки осведомлённости эксперта
|
Баллы |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Осведомлённость эксперта |
Эксперт не знаком с проблемой |
Эксперт плохо знаком с проблемой (проблема входит в сферу его интересов, но ей не занимается) |
Эксперт удовлетворительно знаком с проблемой (непосредственно не участвует в решении данной проблемы) |
Эксперт хорошо знаком с проблемой (участвует в практическом решении проблемы) |
Проблема входит в сферу узкой специализации эксперта |
||||||
Таблица 1.2.4
Анкета оценки компетентности эксперта
|
Вопросы |
О т в е т |
|
Сколько лет Вы работаете в области решаемой проблемы |
до 2-х лет 3 года 4 года – –9лет 10 и более лет
(0,27) (0,32) (0,37)– –(0,66) (0,74)
|
|
Какую научно-организационную работу Вы проводили по решаемой проблеме |
Руководитель Руководитель – – Участник комплекса работ одной работы одной работы по проблеме
(0,70) (0,60) – – – – – (0,39) |
|
Имеете ли Вы учёную степень в области решаемой проблемы |
Доктор наук Кандидат наук Не имеет
(0,65) (0,52) (0,00)
|
|
Какие печатные работы Вы имеете в области решаемой проблемы |
Монография Статьи, Отчёты Не имеете авторские свидетельства (0,65) (0,56) (0,47) (0,00) |
|
Принимали ли Вы участие в международном сотрудничестве в области решаемой проблемы |
Лекции за Доклад на Участие в Не рубежом международной работе - участвовал конференции народной конференции
(0,72) (0,66) (0,60) (0,00) |
|
И так далее
|
– – – – – – – – – – – – – – – – – – – – – – |
Далее эксперту предлагается ответить на вопросы самостоятельной анкеты (табл. 1.2.4). Вопросы более детально характеризуют самого эксперта, его научно-практические достижения, степень участия в решении данной или подобной проблеме, участие в семинарах и научно-практических конференциях по данной проблеме и так далее. По каждому вопросу предлагаются варианты ответов, то есть характеристики компетентности эксперта. Эксперт зачёркивает (отмечает) по своему усмотрению одну из характеристик в каждом вопросе. В анкете для эксперта, в отличие от таблицы 1.2.4, баллы не указываются.
Баллы по конкретной характеристике каждого вопроса заранее определены в анкете для организаторов экспертных оценок по объекту прогнозирования.
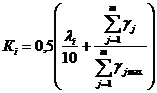
Баллы по данной анкете и по предыдущей анкете самооценки используются для определения компетенции каждого эксперта по формуле 1.2.2.
(1.2.2)
где 
– компетентность i-го эксперта, максимальное значение
коэффициента равно единицы (Кi max =1);
– количество экспертов;
λi – баллы в ячейке, зачёркнутой (отмеченной) i-м
экспертом;
10 – максимальный балл шкалы самооценки экспертов;
γj – балл ответа, зачёркнутый (отмеченный) i-м
экспертом по j-ой характеристике каждого вопроса
анкеты;
γj max – максимальный балл ответа по j-ой характеристике
каждого вопроса анкеты;
– количество вопросов (по одной характеристике в
каждом вопросе) в анкете компетентности экспертов.
Оценив компетентность экспертов, можно определить репрезентативную группу экспертов, то есть необходимое и достаточное количество экспертов в группе.
Сначала определим количество экспертов из условия высокой средней компетентности группы экспертов:
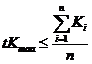, (1.2.3)
где 
– параметр, определяющий репрезентативный объём
статистической выборки. Достаточно взять 2/3 площади
нормального закона распределения, то есть ±2σ или |4σ|;
– максимальная компетентность. В нашем случае,
исходя из формулы 11.3.2., максимальная компетент-
ность равна единице;
– число экспертов;
– компетентность i-го эксперта.
Правая часть уравнения 1.2.3. – средняя компетентность группы экспертов.
Преобразуя формулу 1.2.3., получим количество экспертов в группе, которая характеризуется высокой компетентностью.
, (1.2.4)
Отметим, что может возникнуть необходимость корректировки количества экспертов в группе из условия стабилизации средней оценки прогнозируемого направления. Такая необходимость возникает после процесса прогнозирования, если коэффициент конкордации (согласия) при его оценке окажется несущественным, то есть покажет несущественную взаимосвязь оценок экспертов. В этом случае необходимо исключать эксперта, чья оценка больше всего отличается от средней оценки, и возможно добавлять другого эксперта. Для этого нужно иметь оценки в баллах каждого эксперта по каждому направлению. Данная информация будет получена в процессе прогнозирования, что рассмотрено ниже.
2. Далее нужно получить прогнозные оценим в баллах, по которым можно выбирать направление развития производства и систем управления¸ улучшения качества продукции и др. на предприятии (или прогнозируемой характеристики). Эксперты каждому направлению дают соответствующие баллы в пределах заданной шкалы. По величинам баллов каждому направлению даётся ранг (место) или самим экспертом, или организаторами процесса прогнозирования. Оценки и ранжирование прогнозируемых направлений даны в таблице 1.2.5.
Из таблицы 1.2.5. видно, что наименьшая сумма рангов у первого направления. Поэтому данное направления является наиболее предпочтительным. Для окончательного принятия решения нужно определить коэффициент конкордации (согласия) (
), который изменяется от 0 до 1, и оценить его существенность по одному из критериев теории корреляции.
Таблица 1.2.5.
Оценки и ранжирование прогнозируемых направлений.
|
Эксперты |
Направления |
|||||
|
1 |
2 |
3 |
|
|
||
|
1 |
Балл |
80 |
40 |
60 |
|
50 |
|
Ранг |
1 |
4 |
2 |
|
3 |
|
|
2 |
Балл |
70 |
50 |
80 |
|
60 |
|
Ранг |
2 |
4 |
1 |
|
3 |
|
|
3 |
Балл |
90 |
50 |
70 |
|
80 |
|
Ранг |
1 |
4 |
3 |
|
2 |
|
|
|
Балл |
|
|
|
|
|
|
Ранг |
|
|
|
|
|
|
|
|
Балл |
80 |
50 |
70 |
|
60 |
|
Ранг |
1 |
4 |
2 |
|
3 |
|
|
Сумма рангов |
5 |
16 |
8 |
|
11 |
|
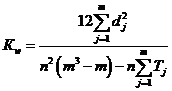, (1.2.5)
где – количество прогнозируемых направлений;
– количество экспертов;
– среднее отклонение по j-ому направлению.
– количество равных связанных (рангов) по j-ому
направлению.
Величину dj можно определить по отклонению оценок экспертов от средней величины в баллах или рангах.
В первом случае среднее отклонение определяется по формуле:
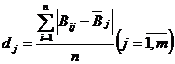, (1.2.6)
где 
– оценка 
-м экспертом 
-го направления;
– средняя оценка j-го направления, данная экспертной
группой.
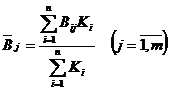, (1.2.7)
Во втором случае среднее отклонение определяется по формуле:
, (1.2.8)
Среднюю сумму рангов определим по формуле:
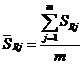, (1.2.9)
Таким образом, определив коэффициент конкордации, нужно оценить его существенность. Для этого используем Z критерий Фишера. Определение его расчётного значения (
) запишем в буквенном обозначении, принятом в данном разделе:
, (1.2.10)
Если расчётное значение Z критерия больше табличного (>
), то мы имеем достаточную согласованность в оценках экспертной группы по прогнозируемым направлениям. Теперь можно принимать окончательное решение о выборе предпочтительного направления. Если <, то процесс прогнозирование на этом не заканчивается.
3. Возникает необходимость корректировки количества экспертов в группе из условия стабилизации средней оценки прогнозируемого направления, что отмечалось в конце первого пункта данного метода прогнозирования. Нужно исключать экспертов, оценки которых в наибольшей степени отличаются от средней величины, и при необходимости включать других экспертов.
Исключение (включение) одного эксперта повлияет на среднюю оценку экспертной группы по прогнозируемому направлению на величину – 
.
, (1.2.11)
где 
– средняя оценка -го направления, данная экспертной
группой после исключения из неё одного 
-го эксперта.
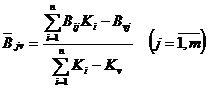, (1.2.12)
где 
– оценка ν-м экспертом -го направления;
– компетентность -го эксперта.
С учётом формулы 1.2.4., получим корректировку количества экспертов в группе, которая будет характеризоваться высокой компетентностью и отвечать условию стабилизации средней оценки прогнозируемого направления.
, (1.2.13)
где 
– максимально возможная оценка j-го направления на
принятой шкале оценок.
Отсюда:
, (1.2.14)
Для стабилизации средней оценки прогнозируемого направления нужно уменьшить величину , что ужесточит требование к отклонению средних величин формулы 1.2.11. и увеличит количество экспертов в группе.
После корректировке количества экспертов в группе следует повторить процесс прогнозирования, определить коэффициент конкордации и оценить его существенность.
Для решения организационно-технической задачи по выбору целей и направлений развития производства, в частности, направлений модернизации или замены оборудования конкретного технологического процесса можно использовать критерии ситуационного управления.
Выбор стратегии предприятия по критериям ситуационного управления рассмотрим на примерах (1÷11).
Постановка задачи для первых восьми примеров (1÷8) следующая. Предприятию следует выбрать стратегию деятельности в отношении варианта развития производства (цель) (Аi,, i=1÷n) при различных вариантах технических возможностей (средств) (Qj, j=l÷m) и заданных ресурсах (aij).
Исходные данные приведены в таблице 1.2.6.
Таблица 1.2.6
Исходные данные для примеров 1 ÷ 8.
|
Варианты развития производства |
Варианты технических возможностей (средств) |
|||||
|
Q1 |
Q2 |
Q3 |
Qj |
minj |
maxj |
|
|
А1 |
3 |
4 |
7 |
а1j |
3 |
7 |
|
А2 |
6 |
2 |
3 |
а2j |
2 |
6 |
|
А3 |
4 |
9 |
2 |
а3j |
2 |
9 |
|
А4 |
8 |
1 |
4 |
а4j |
1 |
8 |
|
Аi |
аi1 |
аi2 |
аi3 |
аij |
|
|
|
maxi |
8 |
9 |
7 |
|
||
В таблице 1.2.6 величины аij – заданные ресурсы в стоимостном выражении. Данные величины могут быть также заданы в виде результатов от реализации вариантов развития производства при различных вариантах технических возможностей (средств): прироста прибыли, экономического эффекта, экономической эффективности и др.
В дальнейших восьми примерах диапазоны изменения переменных, чтобы в дальнейшем в формулах их не повторять, следующие: i=1÷n, j=1÷m.
Пример 1. Предприятию следует выбрать вариант развития производства по критерию «миниминной» стратегии (оптимистическая стратегия).
Аi=mini minj aij=1.
Следовательно, стратегия предприятия по развитию производства соответствует варианту А4.
Пример 2. Предприятию следует выбрать вариант развития производства по критерию «максимаксной» стратегии (пессимистическая стратегия).
Аi=maxi maxj aij=9.
Следовательно, стратегия предприятия по развитию производства соответствует варианту А3.
Следующие два примера соответствуют промежуточному варианту между оптимистической и пессимистической стратегиями.
Пример 3. Предприятию следует выбрать вариант развития производства по критерию «максиминной» стратегии.
Аi=maxi minj aij=3.
Следовательно, стратегия предприятия по развитию производства соответствует варианту А1.
Пример 4. Предприятию следует выбрать вариант развития производства по критерию «минимаксной» стратегии.
Аi=mini maxj aij=6.
Следовательно, стратегия предприятия по развитию производства соответствует варианту А2.
Пример 5. Предприятию следует выбрать вариант развития производства по критерию Гурвица (критерий оптимизма – пессимизма или уравновешенного варианта).
Ai=maxi .
При выборе варианта по критерию Гурвица задается соотношение между оптимистической стратегией (k=1) и пессимистической стратегией (k=0), то есть коэффициент k принадлежит множеству – kЄ.
Перепишем критерий Гурвица следующим образом:
Ai=maxi Gij
,
где Gij=k minj aij+(1-k) maxj aij.
Примем k=0,5. Тогда:
G1=0,5·3+0,5·7=5,0;
G2=0,5·2+0,5·6=4,0;
G3=0,5·2+0,5·9=5,5;
G4=0,5·1+0,5·8=4,5.
Отсюда:
Ai=maxi Gij=5,5.
Следовательно, стратегия предприятия по развитию производства по критерию Гурвица соответствует варианту А3.
Пример 6. Предприятию следует выбрать вариант развития производства по критерию Севиджа.
Ai=mini или
Ai=mini
maxj bij,
где bij=maxi aij–aij.
Определим bij и запишем их значения в таблицу:
|
bj |
maxj |
|||
|
Ai |
5 |
5 |
0 |
5 |
|
2 |
7 |
4 |
7 |
|
|
4 |
0 |
5 |
5 |
|
|
0 |
8 |
3 |
8 |
|
Отсюда:
Ai=mini maxj bij=5.
Следовательно, стратегия предприятия по развитию производства по критерию Севиджа соответствует вариантам А1 и А3.
Пример 7. Предприятию следует выбрать вариант развития производства по критерию Байеса-Лапласа.
m
Ai=maxi∑aij Рj.
j=1
где Рj – вероятность реализации различных вариантах технических
возможностей (средств) (Qj, j=l÷m).
Значения Рj задаются (определяются экспертами). В данном примере: Р1=0,6; Р2 =0,3; Р3 =0,1.
Тогда определим значения
3
Ai=∑aij Рj:
j=1
A1=3·0,6+4·0,3+7·0,1=3,7;
A2=6·0,6+2·0,3+3·0,1=4,5;
A3=4·0,6+9·0,3+2·0,1=5,3;
A4=8·0,6+1·0,3+4·0,1=5,5.
Отсюда:
3
Ai=maxi∑aij Рj=5,5.
j=1
Следовательно, стратегия предприятия по развитию производства по критерию Байеса-Лапласа соответствует варианту А4.
Пример 8. Предприятию следует выбрать вариант развития производства по критерию произведений (Р – критерию).
m
Рi=maxi ∏aij.
j=1
Определим значения
3
Рi=∏aij:
j=1
Р1=3·4·7=84;
Р2=6·2·3=36;
Р3=4·9·2=72;
Р4=8·1·4=32.
Следовательно, стратегия предприятия по развитию производства по критерию произведений соответствует варианту А1.
Пример 9. Предприятию следует выбрать вариант развития производства по критерию минимума суммы рангов экспертов.
n
аi=mini∑Рij (j=1÷m),
i=1
где аi – i-ый вариант стратегии предприятия по развитию производства;
Рij – ранг j-го эксперта по i-му варианту стратегии предприятия по
развитию производства;
n – количество экспертов;
m – количество вариантов стратегии предприятия по развитию
производства.
Результат ранжирования экспертами вариантов стратегии предприятия по развития производства представлен ниже в таблице 1.2.7.
Таблица 1.2.7
Ранжирования экспертами вариантов развития производства.
|
Эксперты |
Варианты развития производства |
||||
|
№ |
Ранг |
а1 |
а2 |
а3 |
а4 |
|
1 |
Р1 |
4 |
3 |
1 |
2 |
|
2 |
Р2 |
3 |
2 |
1 |
4 |
|
3 |
Р3 |
1 |
2 |
4 |
3 |
|
Сумма рангов |
8 |
7 |
6 |
9 |
|
Отсюда:
3
аi=mini∑Рij=6 (j=1÷4),
i=1
Следовательно, стратегия предприятия по развитию производства по критерию минимума суммы рангов соответствует варианту а3.
Пример 10. Предприятию следует выбрать вариант развития производства по критерию минимума суммы отклонений оценок экспертов.
аj=minj (i=1÷n, j=1÷m).
Буквенные обозначения в данной формуле аналогичны буквенным обозначениям предыдущего примера. Исходные данные также соответствуют предыдущему примеру (таблица 6.4).
Определение отклонения оценок экспертов от максимального значения по каждому варианту развития производства аналогично методу, данному в примере 6. Результаты представлены в таблице 1.2.8.
Таблица 1.2.8
Отклонения оценок экспертов от максимального значения
|
Эксперты |
Отклонения оценок экспертов от максимального значения по каждому варианту развития |
|||
|
№ |
а1 |
а2 |
а3 |
а4 |
|
1 |
0 |
1 |
3 |
2 |
|
2 |
1 |
2 |
3 |
0 |
|
3 |
3 |
2 |
0 |
1 |
|
Максималь- ное отклонение |
3 |
2 |
3 |
2 |
Отсюда:
аj=minj = 2 (i=1÷3, j=1÷4).
Следовательно, стратегия предприятия по развитию производства по критерию минимума суммы отклонений оценок экспертов соответствует варианту а2 и а4.
Пример 11. Комбинаторная задача распределения капитальных вложений.
Предприятие хочет развернуть деятельность по четырём направлениям, развития техники на предприятии. На реализацию данной цели предприятие располагает капиталом, который необходимо вложить (распределить) в данные направления таким образом, чтобы суммарная эффективность (норма прибыли, рентабельность и др.) была бы максимальной.
Исходные данные следующие.
1. Величина капитала, которым располагает предприятие, – 4 условные денежные единицы (тысячи или миллионы рублей или долларов).
2. Норма прибыли в зависимости от величины капитальных вложений в каждое направление приведена в таблице 1.2.9.
Таблица 1.2.9
Норма прибыли от капитальных вложений
|
Капвложения
А или Х |
Норма прибыли |
|||
|
f1(X) |
f2(X) |
f3(X) |
f4(X) |
|
|
1 |
0,28 |
0,25 |
0,15 |
0,20 |
|
2 |
0,45 |
0,41 |
0,25 |
0,33 |
|
3 |
0,65 |
0,55 |
0,40 |
0,42 |
|
4 |
0,78 |
0,65 |
0,50 |
0,48 |
Нахождение оптимальной стратегии предприятия по капитальным вложениям в 1-ое и 2-ое направлении соответствует критерию:
F1,2(А) = max .
Результаты расчетов приведены в таблице 1.2.10.
В правом столбце дана максимальная (суммарная) норма прибыли, которая и определит оптимальную стратегию предприятия по капитальным вложениям в каждое из двух направлений в зависимости от заданного объема капитальных вложений.
Аналогично осуществляется нахождение оптимальной стратегии предприятия по капитальным вложениям в 1-ое, 2-ое и 3-ье направлении. Оптимальная стратегия будет соответствовать критерию:
F1,2,3(А) = max .
В этом случае в таблице 1.2.10 вместо f1(X) будет F1,2(Х), а вместо f2(X) будет f3(X).
Соответственно осуществляется нахождение оптимальной стратегии предприятия по капитальным вложениям в 1-ое, 2-ое, 3-ье и 4-ое направлении. Оптимальная стратегия будет соответствовать критерию:
F1,2,3,4(А) = max .
Таблица 1.2.10
Нахождение оптимальной стратегии предприятия в 1-ое и 2-ое направлении
|
А |
Стратегия капвложений |
Х |
f1(X) |
А–Х |
f2(X) |
F1,2(Х) |
Оптимальная стратегия, F1,2(A) |
|
1 1 |
(1,0) (0,1) |
1 0 |
0,28 0 |
0 1 |
0 0,25 |
0,28 0,25 |
0,28 (1,0)
|
|
2 2 2 |
(2,0) (1,1) (0,2) |
2 1 0 |
0,45 0,28 0 |
0 1 2 |
0 0,25 0,41 |
0,45 0,53 0,41 |
0,53 (1,1)
|
|
3 3 3 3 |
(3,0) (2,1) (1,2) (0,3) |
3 2 1 0 |
0,65 0,45 0,28 0 |
0 1 2 3 |
0 0,25 0,41 0,55 |
0,65 0,70 0,69 0,55 |
0,70 (2,1)
|
|
4 4 4 4 4 |
(4,0) (3,1) (2,2) (1,3) (0,4) |
4 3 2 1 0 |
0,78 0,65 0,45 0,28 0 |
0 1 2 3 4 |
0 0,25 0,41 0,55 0,65 |
0,78 0,90 0,86 0,83 0,65 |
0,90 (3,1)
|
Таким образом, будет решена организационно-техническая задача выбора целей и направлений развития производства, в частности, направлений модернизации или замены оборудования конкретного технологического процесса.
Поможем написать любую работу на аналогичную тему