Прогнозирование себестоимости продукции

Как отмечалось, сумма приростов годовых прибылей () за весь расчётный период производства (эксплуатации парка оборудования, ) происходит от снижения себестоимости единицы выпускаемой (реализованной) продукции, увеличения её количества (объёма производства), начиная с первого расчётного года (), и улучшения качества продукции (повышение технического уровня и улучшение качества изготовления продукции).

Зная динамику запланированного (заданного) увеличения выпуска и реализации продукции, определение годового прироста прибыли (эффекта) от влияния данного фактора не вызовет затруднений (формула 2.2.1). Более сложной задачей является определение годового прироста прибыли за счёт снижения себестоимости единицы продукции и улучшения её качества. Для этого необходимо разработать типовую экономико-математическую модель для конкретного вида (-ой) продукции или группы продукции, по которой можно прогнозировать уровень и динамику её себестоимости. Рассмотрим методологию разработки такой модели безотносительно к виду продукции, то есть не будем использовать индекс .

Прежде всего нужно учитывать закономерности в производстве (рис. 3.2.1.).Данные закономерности рассмотрены в работах ряда учёных, в частности, они рассмотрены в работе Саркисяна С.А. .

Закономерность развития технических характеристик продукции (Ух) приводит к росту затрат (себестоимости) на изготовление продукции (Усх). Это не будет являться отрицательным явлением, если эффект (целевая отдача) в натуральном выражении от эксплуатации (использования) продукции (Уэ) будет расти в большей степени, чем рост затрат на её изготовление (Усх). В результате затраты производства на единицу эффекта (Усх/э, удельные затраты) должны снижаться, иначе продукция с экономической точки зрения будет в принципе не эффективна.

В производстве действуют факторы научно-технического прогресса, которые способствуют снижению затрат на изготовление продукции (Усп). Если бы не было влияния фактора развития технических характеристик продукции, то затраты на её изготовление должны снижаться (Усх при Х=соnst). Так как обе группы факторов действуют совместно, то динамика затрат производства (Усхп) на изготовление продукции имеет вид, показанный на рис. 3.2.1. Сначала в большей степени оказывают влияния на рост затрат технические характеристики продукции, когда они находятся в фазе развития. По мере их перехода в фазу морального старения в большей степени начинают оказывать влияние на снижение затрат факторы научно-технического прогресса в производстве.

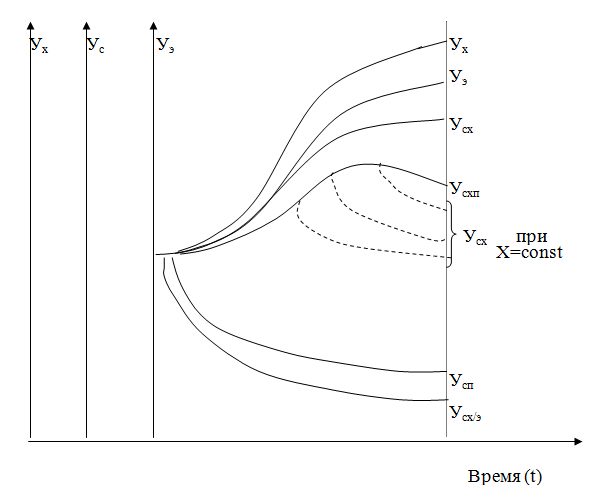
Буквенные обозначения:
Ух – техническая характеристика (показатель) продукции;
Ус – себестоимость изготовления продукции;
Уэ – эффект (целевая отдача) в натуральном выражении от эксплуатации (использования, потребления) продукции.

Рис. 3.2.1. Закономерность развития продукции и производства

Таким образом, рассмотренные закономерности нужно учитывать в процессе прогнозирования себестоимости изготовления продукции на предприятии.

Если об объекте прогнозирования, в данном случае себестоимости продукции, имеется ретроспективная информация, то следует применить статистические методы прогнозирования и разработать экономико-математическую модель. Отметим общие этапы данного процесса прогнозирования.

1. Организация получения ретроспективной информации об объекте прогнозирования.

2. Корректировка ретроспективной информации. Полученная информация, как правило, носит разновремённый характер, так как разновременные этапы жизненного цикла объекта прогнозирования. Для получения типовой модели прогнозирования используется информация по определённому количеству объектов одного класса, у которых сами этапы жизненного цикла осуществлялись в разное время. Поэтому ретроспективную информацию нужно привести, по крайней мере, к моменту применения статистического метода прогнозирования и разработки модели.

3. Логическое формирование факторов, влияющих на поведение объекта. Определение показателей, характеризующих эти факторы. Часто это достаточно сложная задача, так как один фактор может характеризоваться несколькими показателями, а один показатель может характеризовать несколько факторов.

4. Отбор показателей. Часто говорят – отбор факторов. Это некорректная формулировка, так как фактором является общая характеристика, явление и так далее, а для получения модели прогнозирования используются количественные величины, которыми и определяются показатели. Практически нужно определить независимые переменные, которые существенно влияют на целевую функцию объекта прогнозирования. При этом между собой независимые переменные не должны иметь существенную связь.

Отбор показателей можно осуществить с помощью дисперсионного анализа или других методов. Обычно для такого процесса используют прикладные программы.

5. Выбор формы связи между функцией (зависимой переменной) и независимыми переменными. Для этого также существуют прикладные программы. В результате получим соответствующую модель для целей прогнозирования.

Разработанная модель для одного вида продукции имеет ограниченное применение. С её помощью редко возникает возможность осуществлять прогнозирование по другому виду продукции, хотя и того же класса. Поэтому нужно разработать типовую модель, применимую для разного вида продукции одного класса. Рассмотрим решение этой задачи на примере производственных затрат, то есть себестоимости изготовления продукции. Прогнозирование затрат необходимо для экономического обоснования вариантов решаемой задачи. Однако оно может быть использовано для определения направлений улучшения качества продукции, развития производства, улучшения систем управления на предприятии и др.

Предположим, что по ретроспективной информации по трём видам продукции одного класса мы получили аппроксимированные зависимости себестоимости () от времени производства () в кварталах (рис. 3.2.2.). Время производства конечно можно представить и другими измерителями: месяц, год и др. Однако квартал, как правило, – отчётный период.

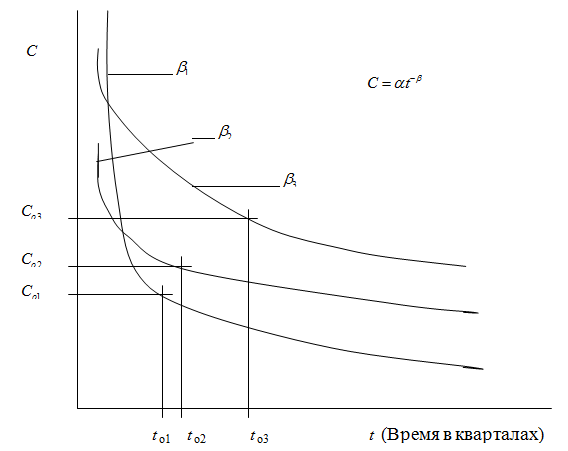
Рис. 3.2.2. Динамика себестоимости производства продукции.

Опыт и дисперсионный анализ показывает, что себестоимость наилучшим образом аппроксимируется по степенной зависимости:

,                                                                                          (3.2.1)

где  и  – параметры уравнения.

Время производства представлено номером квартала с начала производства. Это позволяет себестоимость по видам продукции, которые могли изготавливаться в разное время, представить на графике в одном временном измерении.

На динамику себестоимость продукции влияет не только время производства, но и другие факторы, как, например, масштаб производства. Масштаб производства можно характеризовать такими показателями как суточный выпуск, количество изготовленных изделий по абсолютной величине или нарастающим итогом и др. Однако показатели масштаба производства, как показывает опыт, будут существенно коррелировать с показателем времени производства. Поэтому при необходимости учёта влияния масштаба производства на себестоимость продукции нужно изыскивать искусственный приём косвенного учёта влияния интересуемого показателя. Рассмотрим один из таких приёмов.

Опыт показывает, что себестоимость снижается быстрыми темпами в период серийного освоения производства. В дальнейшем периоде серийно освоенного производства себестоимость снижается медленными темпами. Переход от серийного освоения к серийно освоенному производству условно называют "точкой серийности". Практически это не точка, а определённый период производства, в нашем примере это квартал (). Однако на графике это будет действительно точка (рис. 3.2.3).

Теперь отметим, что в период освоения производства динамика себестоимости зависит от динамики развёртывания производства (рис 3.2.3).

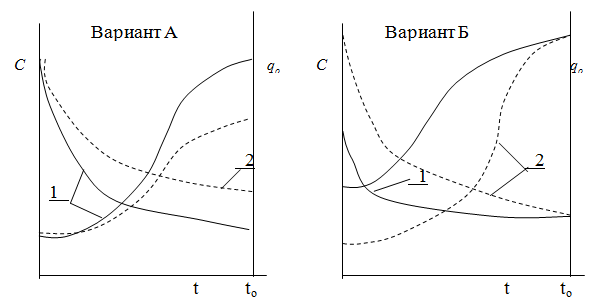
Рис. 3.2.3. Влияние динамики развёртывания производства
на динамику себестоимости продукции

Темпы снижения себестоимости тем больше, чем больше суточный выпуск () в точке серийности (Вариант А, рис. 3.2.3). В начале периода освоения производства уровень себестоимости в первом квартале тем ниже, чем выше суточный выпуск (Вариант Б, рис.3.2.3). Следовательно, динамика себестоимости продукции зависит от соотношения – /, где  – суточный выпуск продукции в первом квартале. В свою очередь, динамику себестоимости характеризует показатель степени . Поэтому задача заключается в получении следующей зависимости:

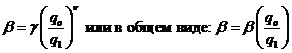,                                        (3.2.2)

Теперь можно уточнить формулу 3.2.1.

                                (3.2.3)

Может возникнуть вопрос об определении точки серийности (). Конечно, можно воспользоваться предыдущим опытом или запланированным периодом освоения производства конкретного вида продукции, но план должен быть обоснованным. Рассмотрим один из методов решения данной задачи для базовой и модифицированной продукции.

Под базовой будем понимать новую продукцию, значительно отличающуюся конструктивно от предыдущей продукции. Под модифицированной будем понимать продукцию, которая имеет прототип (базовую продукцию) и незначительно от неё отличается конструктивно, хотя и имеет улучшенные характеристики (улучшенное качество).

Идея метода заключается в том, что в точке серийности скорость убывания функции (, формула 3.2.1) равна скорости нарастания аргумента (). Для этого должно выполняться условие:

                                                                                     (3.2.4)

В силу разноразмерности функции и аргумента по формуле 3.2.1, данную зависимость выразим в относительных величинах, то есть пронормируем по α, и переведём в проценты:

                                                                                  (3.2.5)

Первую производную приравняем −1;

                                                                          (3.2.6)

Отсюда:

                                                                                 (3.2.7)

Показатель степени  изменяется от 0 до 1. Если построить зависимость  от , то можно заметить, что величина tо достаточно объективна при ≥0,4÷0,5.

Объясняется это тем, что формула 3.2.7 применима для базовой продукции, у которой показатель степени формулы 3.2.1 будет больше 0,5. Величина показателя степени меньше 0,4 характерна для модифицированной продукции, для которой кривая себестоимости не имеет верхней части (рис. 3.2.4).

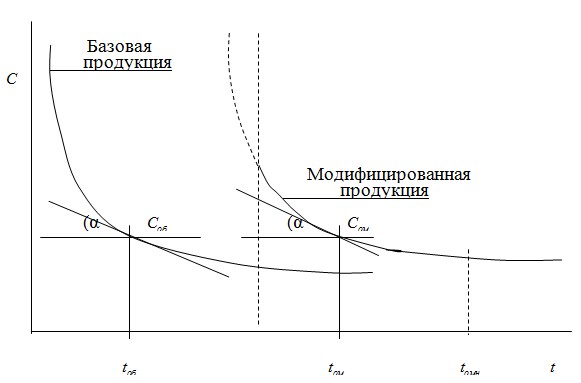
Рис. 3.2.4. Точка серийности базовой и модифицированной продукции

В рисунке 3.2.4 индексами  и  обозначены базовая и модернизированная продукция соответственно.

Дело в том, что у модифицированной продукции большая преемственность от базовой продукции, поэтому кривая себестоимости как бы усечённая. В этих условиях расчётная величина точки серийности () по формуле 3.2.7 значительно отличается от объективной величины . Возникает вопрос, как определить приемлемую величину точки серийности для модифицированной продукции. Метод определения такой величины предложил автор.

Метод заключается в следующем. Нужно метод определения точки серийности для базовой продукции перенести на модифицированную продукцию, учитывая, что динамика её себестоимости, как отмечалось, является усечённой кривой. Для этого нужно приравнять первые производные в точки серийности следующих зависимостей:

                                                                  (3.2.8)

где б, м – индексы базовой и модифицированной продукции.

                                                  (3.2.9)

                                                     (3.2.10)

Отсюда, с учётом формулы 3.2.7, получим:

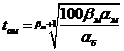                                                                           (3.2.11)

Данный метод можно объяснить по-другому: касательную, проходящую через точку серийности динамики себестоимости базовой продукции, нужно параллельно перенести в качестве касательной динамики себестоимости модифицированной продукции (рис. 3.2.4).

Таким образом, при <0,4 для определения точки серийности следует пользоваться формулой 3.2.11.

Вернёмся к формуле 3.2.3. Её можно рассматривать как экономико-математическую модель для прогнозирования динамики себестоимости различного вида продукции одного класса. Однако модель не учитывает влияние факторов (показателей) на уровень себестоимости данной продукции. Поэтому такую модель ещё нельзя назвать типовой.

В нашем примере (рис .3.2.2) себестоимость трёх видов продукции находятся на различном уровне. Это хорошо видно по величине  в период . Опыт показывает, что на уровень себестоимости влияют изменения конструктивных особенностей продукции, её материалоёмкости и других характеристик.

Подставив  в формулу 3.2.1, получим :

                                                                                      (3.2.12)

Выделим параметр уравнения α и подставим в формулу 3.2.1:

                                                                      (3.2.13)

Теперь в соответствии с общими этапами процесса прогнозирования, отмеченными выше, получим зависимость:

                                                                        (3.2.14)

где    – -ая характеристика продукции;

          – количество характеристик;

      δ, λ – параметры уравнения.

Подставив зависимость по формуле 3.2.14 в формулу 3.2.13 и учтя зависимость по формуле 3.2.3, получим:

                                                          (3.2.15)

Данная формула является типовой экономико-математической моделью, по которой можно прогнозировать уровень и динамику себестоимости производства разного вида модифицированной или новой продукции определённого класса (группы).