Явления переноса.

Теплопроводность: перенос теплоты. Теплопроводность не зависит от давления и увеличивается пропорционально корню квадратному из температуры. В этом случае  (см. вопрос про вязкость) есть средняя энергия теплового движения, приходящаяся на одну молекулу. Плотность потока теплоты:.

Коэффициент теплопроводности: ,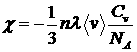

 – концентрация,  – молярная теплоёмкость ( – число степеней свободы),  – длина свободного пробега.

Замечания: 1) 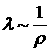, не зависит от давления; 2) .

Диффузия: движение вещества компонент, составляющих фазу, связанное с отклонением плотности системы. – плотность диффузионного потока (кол-во вещ-ва, проходящего перпендикулярно единице площади в ед. времени).  – закон Фика.

Коэффициент диффузии: 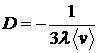,  – длина свободного пробега, – средняя скорость.

Замечания: 1) 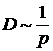,  – давление; 2) .

Вязкость: возникновение сил трения в газах и жидкостях обусловлено процессом переноса импульса упорядоченным движеним молекул. Быстрее движущийся слой замедляется, а медленнее движущийся – ускоряется. . Кинематическая вязкость – динамическая вязкость, отнесённая к плотности.

Пусть  характеризует некоторое молекулярное свойство, отнесённое к одной молекуле. Этим свойством может быть энергия, импульс, концентрация. Если в равновесном состоянии  постоянно по всему объёму, то при наличии градиента  имеет место движение  в направлении его уменьшения. Пусть ось  направлена вдоль градиента . Среднее расстояние, пробегаемое молекулами, пересекающими площадку  после последнего столкновения, равно 2<l>3.  – импульс, передаваемый в единицу времени от слоя к слою через единицу поверхности, т.е. плотность потока импульса.

,  – скорость движения газа как целого.

.

Замечания: 1)  не зависит от давления; 2) .

Потоки всех величин являются алгебраическими. Их знак зависит от направления оси . Достаточно обратить направление этой оси на противоположное, и знак потока изменится.

Во всех явлениях переноса направления плотностей потоков противоположны градиентам соответствующих величин. Это означает, что потоки всегда направлены в сторону уменьшения величин , , , т.е. против их градиентов. Таким образом, для потоков существенны градиенты величин, имеющих тенденцию выравниваться.