Задача: найти уравнение для интеграла столкновения частиц.
Предположения:
I. Рассматриваем только парные взаимодействия, где радиус действия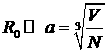 
, время столкновения 
– рассматриваем пространственно однозначные системы. 
.
II. Решение будем искать виде статистических функций 
, т.е. функций, определяющих число частиц в объёме 
. Исходить будем из первого ур-я цепочки Боголюбова (также можно получить из законов сохр. энергии и импульса).
(1) 
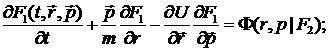
зависит от 
через зависимость 
от .
Пусть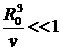 
, используем принцип ослабления:
(2) 
; 
. Запишем ур-е Лиувилля для 2-х частиц:
(3) 
.
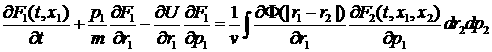(4) 
.
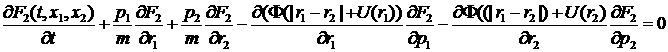Далее используем условие эволюции; полагая 
, 
. Упрощая (4) и подставляя выражение для в (3).
Интеграл столкновения (кинетическое ур-е) Больцмана:
(5) 
Н-теорема Больцмана.
Введём: 
и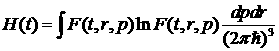 
.
Исследуем знаки производных 
и 
. После преобразований придем к неравенству:
.
Уравнение Больцмана описывает необратимую во времени эволюцию системы.
Поможем написать любую работу на аналогичную тему