Атом водорода

В атоме водорода или водородоподобном ионе потенциальная энергия электрона равна  где Ze — заряд ядра, r — расстояние между ядром и электроном.

Уравнение Шредингера имеет в этом случае вид  (1)

Поскольку поле является центрально-симметричным, удобно воспользоваться сферической системой координат: r, , . Подставив в (1) выражение оператора Лапласа в сферических координатах, получим уравнение:

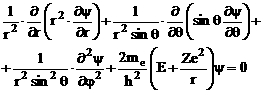           (2)

Можно показать, что уравнение (2) имеет требуемые (т. е. однозначные, конечные и непрерывные) решения в следующих случаях: 1) при любых положительных значениях Е; 2) при дискретных отрицательных значениях энергии, равных  (n=1, 2, 3,…).          (3)

Случай Е > 0 соответствует электрону, пролетающему вблизи ядра и удаляющемуся вновь на бесконечность. Случай Е < 0 соответствует электрону, находящемуся в пределах атома. Сравнение (3) с (5) показывает, что квантовая механика приводит к таким же значениям энергии водородного атома, какие получались и в теории Бора. Однако в квантовой механике эти значения полу- чаются логическим путем из основного предположения о том, что движение микрочастиц описывается уравнением Шредингера. Бору же для получения такого результата пришлось вводить специальные дополнительные предположения.

Собственные функции уравнения (2) содержат три целочисленных параметра. Один из них совпадает с номером уровня энергии п, два других принято обозначать буквами l и т. Эти числа называются квантовыми:

п — главное квантовое число,

l — азимутальное квантовое число,

т — магнитное квантовое число.

При данном п числа l и т могут принимать следую» щие значения:

L = 0, 1, 2, …, п -1,

т. е. всего п различных значений;

т=-l, -l+1, .... -1, 0, +1, .... l-1, l,

т. е. всего 2l + 1 различных значений.

Таким образом, каждому Еп (кроме Е1) соответствует несколько волновых функций  отличающихся значениями квантовых чисел l и т. Это означает, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях.

Состояния с одинаковой энергией называются вырожденными, а число различных состояний с каким-либо значением энергии называется кратностью вырождения соответствующего энергетического уровня.

Кратность вырождения уровней водорода легко вычислить, исходя из возможных значений для l и т. Каждому из п значений квантового числа l соответствует 2l + 1 значений квантового числа т. Следовательно, число   различных состоя-

ний, соответствующих данному п, равно

Таким образом, каждый уровень энергии водородного атома имеет вырождение кратности п2.

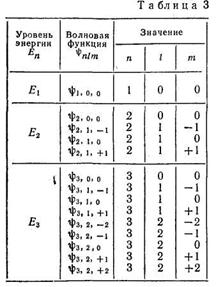
В табл. 3 приведены состояния, соответствующие первым трем энергетическим уровням.

Как мы выяснили, состояние электрона в водородном атоме зависит от трех квантовых чисел п, l и т, причем значение главного квантового числа п. определяет энергию состояния. Естественно предположить, что и два других квантовых числа определяют какие-то физические величины. Действительно, в квантовой механике доказывается, что азимутальное квантовое число l определяет величину момента импульса электрона в атоме, а магнитное квантовое число т — величину проекции этого момента на заданное направление в пространстве. Под заданным направлением (мы будем обозначать его буквой z) понимают направление, выделенное физически,путем создания, например магнитного или электрического поля.

Момент импульса М оказывается равным:       (4)

Проекция момента импульса на заданное направление равна: Мz = mh.     (5)

Соотношения (4) и (5) показывают, что момент импульса электрона в атоме и проекция этого момента являются, как и энергия, квантованными величинами. Постоянную h можно рассматривать как естественную единицу момента импульса.

Итак, состояния с различными значениями азимутального квантового числа l отличаются величиной момента импульса. В атомной физике применяются заимствованные из спектроскопии условные обозначения состояний электрона с различными значениями момента импульса. Электрон, находящийся в состоянии с l = 0, называют s-электроном (соответствующее состояние — s-состояни-ем), с l = 1 — р-электроном, с l = 2 — d-электроном, с l = 3 — f-электроном, затем идут g, h и т. д. уже по алфавиту. Значение главного квантового числа указывается перед условным обозначением квантового числа l. Таким образом, электрон в состоянии с п = 3 и l = 1 обозначается символом Зр и т. д.

Поскольку l всегда меньше п, возможны следующие состояния электрона:

1s

2s, 2p,

3s, 3p, 3d,

4s, 4p, 4d, 4f

и.т.д.

Схему уровней энергии можно изобразить пользуясь схемой, показанной на рис. 1. На этой схеме отражено (правда, частично) вырождение уровней; кроме того, она имеет еще ряд существенных преимуществ, которые вскоре станут очевидными.

Мы знаем, что испускание и поглощение света происходит при переходах электрона с одного уровня на другой. В квантовой механике доказывается, что возможны только такие переходы, при которых квантовое число / изменяется на единицу: . (6)

Условие, выраженное соотношением (6), называется правилом отбора. Существование правила (6) обусловлено тем, что фотон обладает собственным моментом импульса (спином), равным примерно h (в дальнейшем мы уточним его значение). При испускании фотон уносит из атома этот момент, а при поглощении привносит, так что правило отбора (6) есть просто следствие закона сохранения момента импульса.

На рис. 198 показаны переходы, разрешенные правилом (6). Пользуясь условными обозначениями состояний электрона, переходы, приводящие к возникновению серии Лаймана, можно записать в виде:

np1s    (n = 2, 3, ...); серии Бальмера соответствуют переходы:

ns2p и nd2p    (n = 3, 4, ...),

и т. д.

Состояние 1s является основным состоянием атома водорода. В этом состоянии атом обладает минимальной энергией. Чтобы перевести атом из основного состояния в возбужденное (т. е. в состояние с большей энергией), ему необходимо сообщить энергию. Это может быть осуществлено за счет теплового соударения атомов (по этой причине нагретые тела светятся — атомы излучают, возвращаясь из возбужденного в основное состояние), или оптического возбуждения. Кроме обозначенных квантовых чисел имеет место спиновое квантовое число, характеризующее собственный механический момент электрона в атоме.