Теорема о циркуляции вектора индукции магнитного поля.

Рассмотрим провод с током, выделим в нем прямолинейный участок и выделим в нем замкнутый контур .

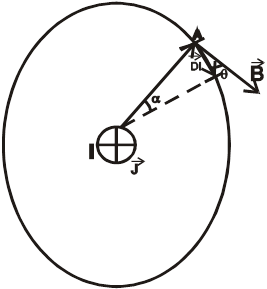
Зафиксируем некую точку , проведем к ней радиус вектор. В этой точке провод будет создавать магнитное поле. Из точки  построим прямолинейный участок контура .

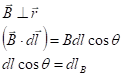
 – очень маленький, поэтому

Выполним такое разбиение для каждого участка контура и просуммируем, учтя, что индукция магнитного поля, созданного длинным проводом равна: .

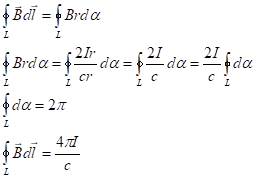
Пусть теперь имеется много проводов, и они пересекают поверхность, натянутую на контур .

.

Суммирование идет по , а интегрирование идет по , поэтому суммирование интегрирование можно поменять местами.

.

Циркуляция вектора магнитной индукции  по произвольному замкнутому контуру, равна сумме всех токов, пересекающих поверхность, натянутую на этот контур с коэффициентом .

Обобщим. Пусть у нас имеется среда, в которой некотором образом текут токи. Они определены в каждой точке вектором плотности тока .

Выберем произвольный замкнутый контур . Разбив его на маленькие кусочки, можно считать, что внутри кусочка . Тогда . Поэтому . Тогда теорема о циркуляции может быть записана следующим образом:

.

Пусть имеется среда и контур . Натянем на этот контур поверхность. Тогда, согласно теореме Стокса, циркуляцию вектора  по замкнутому контуру можно представить как поток ротора вектора  через поверхность, натянутую на данный контур.

.

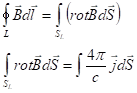Имеем два интеграла одного смысла (поток) по одной и той же поверхности, поэтому:

.

Теорема о циркуляции вектора .

Пример. Поле длинного соленоида (катушки).

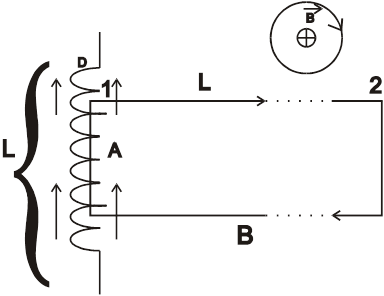
Найдем индукцию магнитного поля внутри катушки (внутри катушки поле  параллельно оси катушки). Катушка такова, что диаметр сечения катушки много меньше длины катушки.

Выберем замкнутый контур в форме прямоугольника, одна сторона которого находится внутри катушки, другая – на бесконечности. Запишем теорему о циркуляции:

.

Если контур не очень большой по сравнению с длинной соленоида, то внутри поле можно считать одинаковым.

.

По боковым сторонам циркуляция равна нулю, так как направление обхода контура перпендикулярно направлению вектора магнитной индукции  внутри соленоида. По второй стороне прямоугольника, параллельной оси соленоида, циркуляция вектора  равна нулю, так как эта сторона находится на бесконечности.  – количество витков, которые охватил контур. Допустим, что намотка такова, что на единицу длины приходится  витков. Тогда: и . Получили поле внутри соленоида:

.