Возьмем контур, охватывающий прямой ток, и вычислим для него циркуляцию вектора В:
![]()
В начале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор ![]() направлен по касательной к окружности, проходящей через эту точку (линии
направлен по касательной к окружности, проходящей через эту точку (линии ![]() прямого тока – окружности).
прямого тока – окружности).
Воспользуемся свойствами скалярного произведения векторов.
![]() где
где ![]() – проекция dl на вектор
– проекция dl на вектор ![]() , но
, но ![]() , где R – расстояние от прямой тока I до dl.
, где R – расстояние от прямой тока I до dl.
![]() .
.
Отсюда
|
|
|
|
это теорема о циркуляции вектора ![]() : циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.
: циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.
Иначе обстоит дело, если ток не охватывается контуром (рис. 2.9).
При обходе радиальная прямая поворачивается сначала в одном направлении (1–2), а потом в другом (2–1). Поэтому ![]() , и следовательно
, и следовательно
|
|
|
|
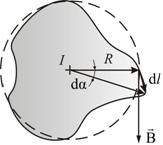
Рис. 2.9
Итак, ![]() , где I – ток, охваченный контуром L.
, где I – ток, охваченный контуром L.
Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы.
Если контур охватывает несколько токов, то
|
|
|
|
т.е. циркуляция вектора ![]() равна алгебраической сумме токов, охваченных контуром произвольной формы.
равна алгебраической сумме токов, охваченных контуром произвольной формы.
Теорема о циркуляции вектора индукции магнитного поля ![]() позволяет легко рассчитать величину В от бесконечного проводника с током (рис. 2.10):
позволяет легко рассчитать величину В от бесконечного проводника с током (рис. 2.10): ![]() .
.
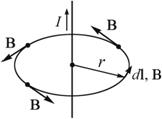
Рис. 2.10
Итак, циркуляция вектора магнитной индукции ![]() отлична от нуля, если контур охватывает ток (сравните с циркуляцией вектора
отлична от нуля, если контур охватывает ток (сравните с циркуляцией вектора ![]() :
: ![]() ).
).
Такие поля, называются вихревыми или соленоидальными.
Поможем написать любую работу на аналогичную тему
Реферат
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора магнитной индукции)
От 250 руб
Контрольная работа
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора магнитной индукции)
От 250 руб
Курсовая работа
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора магнитной индукции)
От 700 руб


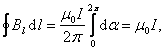 ,
,