Граничные условия для векторов  и  на границах раздела двух сред.

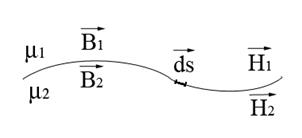
Рассмотрим две полу бесконечные среды, состоящие из двух магнетиков, которые возможно являются проводниками. Один магнетик характеризуется магнитной проницаемостью , а другой . Поле характеризуется функцией , по границе раздела возможно течет ток .

Выберем площадку  на границе раздела двух сред.  на столько мала, что плотность тока на ней можно считать постоянной, и поле  по разные стороны от площадки  тоже постоянно. Зададим вектор нормали  и запишем т. Гаусса для вектора : .

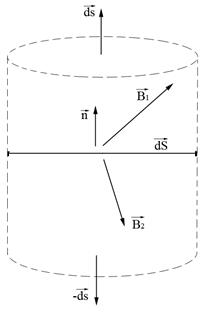Выдерем поверхность  в виде цилиндра с основанием  и высотой . Запишем поток вектора  через поверхность : .

Устремим  к нулю, тогда ,  

, где  - нормальная компонента вектора .

С учетом того, что основания цилиндра имеют разные направления нормали, а мы хотим записать в проекции на вектор , то , т.о. получаем граничные условия вектора :

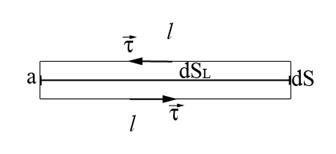Выбреем замкнутый контур в виде прямоугольника со сторонами  и  и запишем теорему о циркуляции для вектора  по данному замкнутому контуру : .

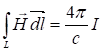Поскольку вблизи площадки вектора  и  постоянны, то можем не писать интеграл, и т.к. , то  

Если , то .

 - поток вектора  через замкнутую поверхность .

Введем вектор линейной плотности тока - ток на единицу длинны, тогда .  Таким образом получаем формулу

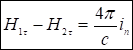
На границе раздела двух сред вектор  прерывается и величина этого раздела с точностью до коэффициента равна нормальной компоненте линейной плотности тока проводимости (от батарейки).

Замечания:

1.      !!!

2.     Для вектора  можно написать формулу похожую на , но в нее будут входить молекулярные токи, а что с ними делать – не знаем – бесполезная формула!