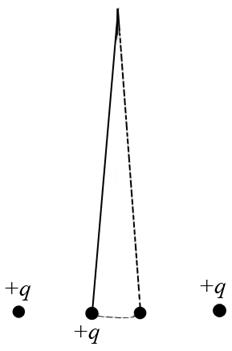
Представим, что шарик движется в двух полях, н.р. заряженный математический маятник рядом с которым симметрично расположены заряды одинакового знака. Шарик движется финитно. В этом случае шарик не обязательно будет совершать гармонические колебания, даже если обе ямы параболические. Процесс нахождения результирующего колебания называется сложение колебаний. Суммарное колебание зависит от характера колебаний. До этого мы рассматривали колебания скалярной величины, но может колебаться и вектор, а скаляр – это его проекция. Суммарное колебание зависит она 
- одинаковая она или разная.
Пусть отдельно уравнения колебаний для гравитационного и кулоновского поля имеют вид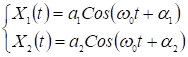 
- одинаковые, но разные начальные фазы колебаний.
Итак, сумма двух гармонических колебаний с одинаковой частотой есть гармонические колебания.
Посмотрим, как складываются гармонические колебания с разными частотами.
Разберем частный случай: 
и 
чуть-чуть отличаются друг от друга. Пусть амплитуды и начальные фазы колебаний одинаковы.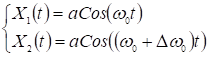 
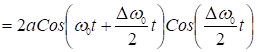
при 
.
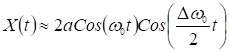Точная настройка двух струн на гитаре означает, что мы стремим 
, 
, т.е. 
.
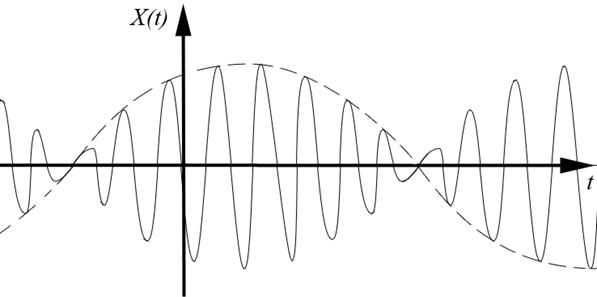
Если гитара расстроена, то 
- значительно, и две струны, расположенные рядом, издают звук похожий на «ау-ау» с периодом 
.
Результат сложения двух близких по частоте колебаний называется биение. Если частоты хотя бы немного различаются, то колебания становятся не гармоническими (биения).
Колеблющиеся вектора, колеблются в перпендикулярных векторах.
.
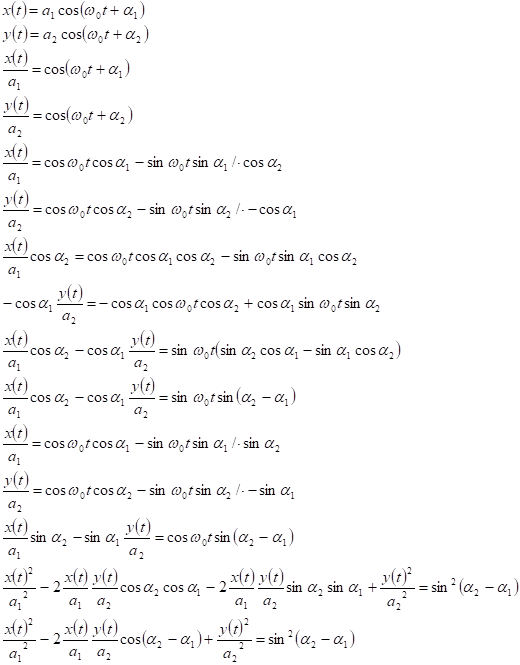Получили уравнение эллипса, полуоси которого расположены под углом к осям координат.
.
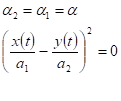
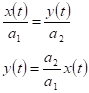По данной траектории колеблется конец вектора, являющийся суммой двух взаимно перпендикулярных рассматриваемых векторов. Конец этого вектора колеблется от начала координат на расстоянии 
.
.
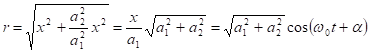Результирующее движения является гармоническим колебанием той же частоты.
.
.
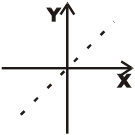
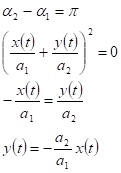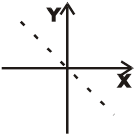
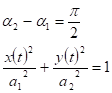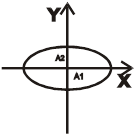
Получили каноническое уравнение эллипса.
Поможем написать любую работу на аналогичную тему