Резонанс.

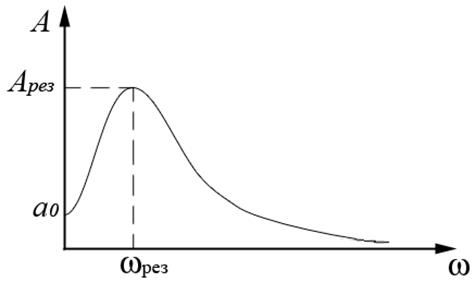
Посмотрим как зависит амплитуда установившихся колебаний от частоты силы.

;

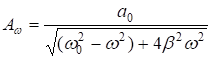Найдём экстремум 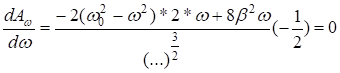. Откуда  - при такой  имеет место быть экстремум. Т.к. он единственный  что это максимум и амплитуда колебаний будет максимальна.  определяется  - самим осциллятором и вязкостью среды. Ситуация, когда амплитуда вынужденных колебаний достигает максимума – резонанс.

.

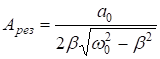1.      , т.е. колебания станут нелинейными.

2.     Чем вязкость меньше, тем график амплитуды пойдёт выше.

Найдём такую частоту, при которой 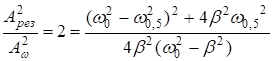. Предположим, что резонансная кривая симметрична и , т.е. затухание малое. Тогда

;

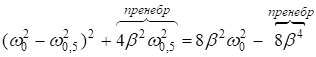, но т.к. кривая узкая то , но

;

;

.

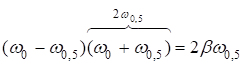Т.о. для систем с малым затуханием выполняется соотношение .

 - величина на которую нужно отступить в право или в лево от резонанса, чтобы колебаний уменьшилась в два раза.

Величина,  называется логарифмический декремент затухания

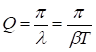 - добротность.

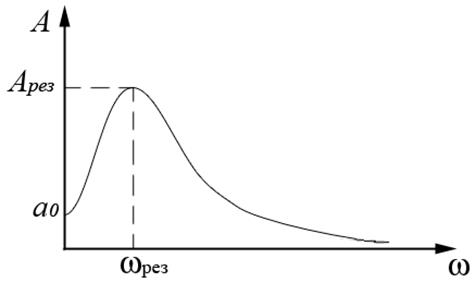Найдем отношение высоты резонансной кривой к :

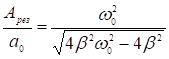
Пусть максимум узкий, тогда     

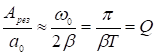
Добротность – это безразмерная величина.

Ее смысл: Если есть вынуждающая сила, то чем больше вязкость, тем меньше максимум. Добротность показывает во сколько раз можно увеличить  по отношению к смещению постоянной силы. Чем больше добротность ,тем больше , чем меньше добротность , тем меньше . Показывает во сколько раз можно увеличить амплитуду маятника по отношению к смещению силы. Чем добротность больше, тем пик выше.

Фазовые характеристики резонанса.

Установившиеся колебания 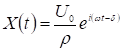 повторяют действующую силу  не точно, а отстают по фазе на величину .

Посмотрим, в каком случае .

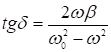 - в разных точках кривой начальная фаза колебаний будет разной.  зависит от затухания  и свойства самого осциллятора . Построим график .

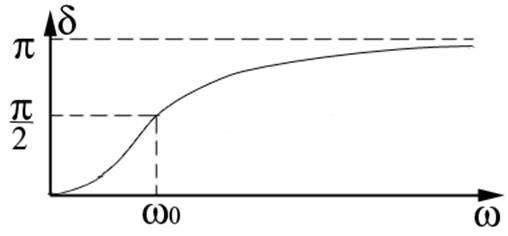
Три вспомогательные точки:

Чем больше частота , тем больше отставание маятника от силы.

При  отставание стремится к половине периода.

Запишем дифференциальные уравнения для колебательного контура.

Соберем электрическую цепь.

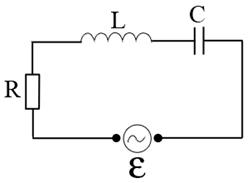
Найдем уравнения, которые описывают заряд на конденсаторе .

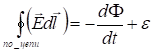 будем работать в СИ. Считаем, что ток в данной системе квазистационарный, т.е в заданный момент времени токи во всех точках цепи одинаковые.         (1)

При записи выражения (1) считали, что катушка не деформируется и её индуктивность  постоянна, а это значит, что .

Запишем выражение (1) в другом виде   и сравним с уже известным уравнением . Эти уравнения имеют одинаковый вид. Поэтому, если в формулах, полученных для механических колебаний, заменим константы  и , то они будут справедливы для уравнения .

 - величина на которую нужно отступить в право или в лево от резонанса, чтобы колебаний уменьшилась в два раза.

Величина,  называется логарифмический декремент затухания

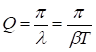 - добротность.

Найдем отношение высоты резонансной кривой к :

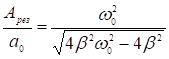
Пусть максимум узкий, тогда     

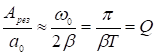
Добротность – это безразмерная величина.

Ее смысл: Если есть вынуждающая сила, то чем больше вязкость, тем меньше максимум. Добротность показывает во сколько раз можно увеличить  по отношению к смещению постоянной силы. Чем больше добротность ,тем больше , чем меньше добротность , тем меньше . Показывает во сколько раз можно увеличить амплитуду маятника по отношению к смещению силы. Чем добротность больше, тем пик выше.

Фазовые характеристики резонанса.

Установившиеся колебания 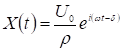 повторяют действующую силу  не точно, а отстают по фазе на величину .

Посмотрим, в каком случае .

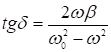 - в разных точках кривой начальная фаза колебаний будет разной.  зависит от затухания  и свойства самого осциллятора . Построим график .

Три вспомогательные точки:

Чем больше частота , тем больше отставание маятника от силы.

При  отставание стремится к половине периода.

Запишем дифференциальные уравнения для колебательного контура.

Соберем электрическую цепь.

Найдем уравнения, которые описывают заряд на конденсаторе .

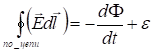 будем работать в СИ. Считаем, что ток в данной системе квазистационарный, т.е в заданный момент времени токи во всех точках цепи одинаковые.         (1)

При записи выражения (1) считали, что катушка не деформируется и её индуктивность  постоянна, а это значит, что .

Запишем выражение (1) в другом виде   и сравним с уже известным уравнением . Эти уравнения имеют одинаковый вид. Поэтому, если в формулах, полученных для механических колебаний, заменим константы  и , то они будут справедливы для уравнения .