В диэлектриках источниками поля кроме сторонних являются также и связанные заряды. Поэтому теорема Гаусса для ![]() запишется:
запишется:
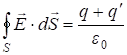 . (2.24)
. (2.24)
Так как из (2.23) ![]() , то:
, то: ![]() . Тогда:
. Тогда:
![]() , или
, или
![]() . (2.25)
. (2.25)
Если ввести вектор ![]() , то электрическая индукция
, то электрическая индукция ![]() измеряется в тех же единицах, что и
измеряется в тех же единицах, что и ![]() , т.е. в Кл/м2,
, т.е. в Кл/м2, ![]() - В/м, и из (2.25) получим:
- В/м, и из (2.25) получим:
![]() . (2.26)
. (2.26)
Это теорема Гаусса для вектора ![]() .
.
Поток вектора ![]() через замкнутую поверхность равен стороннему заряду, заключенному внутри этой поверхности.
через замкнутую поверхность равен стороннему заряду, заключенному внутри этой поверхности.
Видно, что единственным источником ![]() являются свободные заряды. Вектор
являются свободные заряды. Вектор ![]() начинается на
начинается на ![]() и заканчивается на
и заканчивается на ![]() .
.
Учтем, что: ![]() (2.19), тогда:
(2.19), тогда:
![]() , (2.27)
, (2.27)
![]() - (2.28)
- (2.28)
диэлектрическая проницаемость.
Применив (2.26) для точечного заряда, получим:
![]() ;
; ![]() .
.
![]() . (2.29)
. (2.29)
Если учесть, что ![]() , то напряженность поля точечного заряда в диэлектрике:
, то напряженность поля точечного заряда в диэлектрике:
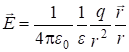 , (2.30)
, (2.30)
то есть внутри диэлектрика поле в ![]() раз меньше, чем в вакууме. Именно с рассмотрения вопроса, почему поле в диэлектрике меньше, чем внешнее (или поле в вакууму) и начиналось изучение электрического поля в диэлектрике (§2.3). Отсюда ясен физический смысл
раз меньше, чем в вакууме. Именно с рассмотрения вопроса, почему поле в диэлектрике меньше, чем внешнее (или поле в вакууму) и начиналось изучение электрического поля в диэлектрике (§2.3). Отсюда ясен физический смысл ![]() . Во столько же раз меньше и потенциал точечного заряда:
. Во столько же раз меньше и потенциал точечного заряда:
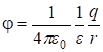 . (2.31)
. (2.31)
Тогда, емкость конденсатора при наличии диэлектрика в ![]() раз больше емкости, между пластинами которой содержится вакуум.
раз больше емкости, между пластинами которой содержится вакуум.
Рассмотрим теперь граничные условия для ![]() на границе двух диэлектриков.
на границе двух диэлектриков.
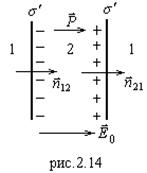 На границе двух диэлектриков (рис.2.14) в поле
На границе двух диэлектриков (рис.2.14) в поле ![]() возникают связанные заряды. Имеются две границы – 1-2 и 2-1 и две нормали на границе
возникают связанные заряды. Имеются две границы – 1-2 и 2-1 и две нормали на границе ![]() и
и ![]() . Они и показывают, какую границу мы рассматриваем.
. Они и показывают, какую границу мы рассматриваем.
1. Рассмотрим границу 1-2 (рис.2.15). Нормаль ![]() положительна, при этом
положительна, при этом ![]() (например, воздух-диэлектрик).
(например, воздух-диэлектрик).
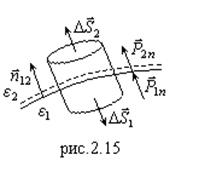 Чтобы вывести условия для нормальных составляющих, используем теорему Гаусса. В качестве замкнутой поверхности рассмотрим цилиндр (рис.2.15), для которого:
Чтобы вывести условия для нормальных составляющих, используем теорему Гаусса. В качестве замкнутой поверхности рассмотрим цилиндр (рис.2.15), для которого:
![]() ,
, ![]() .
.
Тогда из (2.23), ![]() - связанные заряды.
- связанные заряды.
![]() , (2.32)
, (2.32)
но так как ![]() , то из (2.19) следует, что:
, то из (2.19) следует, что:
![]() ,
, ![]() .
.
Тогда ![]() , что и видно из рис.2.14.
, что и видно из рис.2.14.
Если ![]() , т.е. на границе нет сторонних зарядов, то, применив (2.26) и (2.24), получим:
, т.е. на границе нет сторонних зарядов, то, применив (2.26) и (2.24), получим:
![]() , (2.33)
, (2.33)
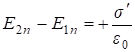 . (2.34)
. (2.34)
Но так как ![]() , то
, то ![]() . Это согласуется с результатами для
. Это согласуется с результатами для ![]() . С учетом знака
. С учетом знака ![]() для границы 1-2 запишем граничные условия (2.32-2.34):
для границы 1-2 запишем граничные условия (2.32-2.34):
![]() ,
,
![]() ,
,
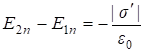 .
.
Так как ![]() , то:
, то:
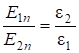 . (2.35)
. (2.35)
2. Рассмотрим границу 2-1 (рис.2.16): ![]() .
.
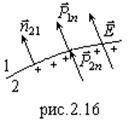 Используя теорему Гаусса как и на границе 1-2 и учтя, что
Используя теорему Гаусса как и на границе 1-2 и учтя, что ![]() ,
, ![]() , получим:
, получим:
![]() ;
;
![]() ;
; ![]() ;
;
Тогда: ![]() ; при этом
; при этом ![]() , что согласуется с рис.2.14. Чтобы найти тангенциальные составляющие, используем теорему о циркуляции вектора
, что согласуется с рис.2.14. Чтобы найти тангенциальные составляющие, используем теорему о циркуляции вектора ![]() (1.27). Выбрав контур в виде прямоугольника абвг, получим условие для
(1.27). Выбрав контур в виде прямоугольника абвг, получим условие для ![]() .
.
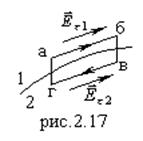
![]() ;
;
![]() ;
;
![]() . (2.36)
. (2.36)
Подставляя выражения для 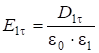 и
и 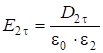 , получим:
, получим:
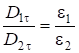 . (2.37)
. (2.37)
При ![]()
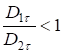
![]()
![]() ;
; ![]() .
.
Преломление силовых линий на границе.
Возьмем, как и прежде ![]() , тогда: из (2.35) и (2.36):
, тогда: из (2.35) и (2.36):
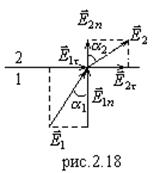
![]() ,
, ![]() ,
,
а также из (2.32):
![]() ,
, ![]() ,
,
Поэтому углы ![]() (см. рис.2.18).
(см. рис.2.18).
Тогда ![]() , т.к.
, т.к.
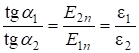 . (2.38)
. (2.38)
Силовые линии поля ведут себя, как показано на рис.2.18, т.е. преломляются на границе.
Пример.
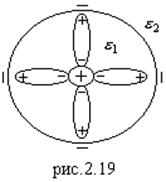 Точечный заряд
Точечный заряд ![]() находится в центре шара из диэлектрика с проницаемостью
находится в центре шара из диэлектрика с проницаемостью ![]() . Радиус шара
. Радиус шара ![]() . Шар окружен безграничным диэлектриком с проницаемостью
. Шар окружен безграничным диэлектриком с проницаемостью ![]() (рис.2.19). Найти
(рис.2.19). Найти ![]() на границе диэлектрика и связанный заряд внутри шара.
на границе диэлектрика и связанный заряд внутри шара.
Напряженность поля как функция расстояния ![]() от центра шара по теореме Гаусса для
от центра шара по теореме Гаусса для ![]() (2.26) и формуле (2.27) запишем:
(2.26) и формуле (2.27) запишем:
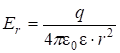 .
.
Тогда:
![]() ; и
; и
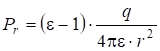 . (2.39)
. (2.39)
На границе 1-2 между диэлектриками:
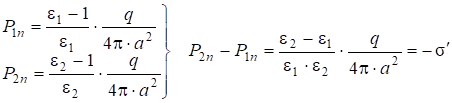 . (2.40)
. (2.40)
Видим, что знак ![]() зависит от соотношения между
зависит от соотношения между ![]() и
и ![]() . При
. При ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Внутри шара при
. Внутри шара при ![]() из (2.23):
из (2.23):
![]() .
.
Подставив (2.39), получим:
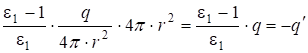 . (2.41)
. (2.41)
Видно, что внутри шара всегда появляется связанный заряд ![]() , если заряд
, если заряд ![]() .
.
Поможем написать любую работу на аналогичную тему

