Из выше рассмотренного ясно, что в зависимости от того, где расположится уровень Ферми (внутри разрешенной зоны энергий или в запрещенной зоне), заполнение зон будет различным.
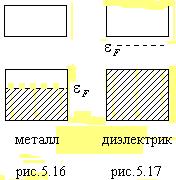
Различие между металлами и диэлектриками (полупроводниками) связано с заполнением зон. Если энергия Ферми ![]() находится внутри нижней (валентной) зоны на рис.5.16, то эта зона заполнена не полностью а верхняя зона полностью свободна. Если зона заполнена не полностью, то в ней есть свободные уровни, на которые под действием электрического поля могут перейти электроны, значит такое вещество является проводником (металлом). Проводимость осуществляется электронами в валентной зоне по схеме, описанной выше (см.рис.5.12).
находится внутри нижней (валентной) зоны на рис.5.16, то эта зона заполнена не полностью а верхняя зона полностью свободна. Если зона заполнена не полностью, то в ней есть свободные уровни, на которые под действием электрического поля могут перейти электроны, значит такое вещество является проводником (металлом). Проводимость осуществляется электронами в валентной зоне по схеме, описанной выше (см.рис.5.12).
 Если энергия Ферми
Если энергия Ферми ![]() находится внутри запрещенной зоны (рис.5.17), то валентная зона заполнена полностью, а верхняя так же, как и в предыдущем случае, полностью свободна. При наложении электрического поля движение электрона невозможно, так как невозможен его переход с уровня на уровень – все уровни энергии заняты. Значит, невозможно возникновение электрического тока в цепи с веществом, имеющим такое электрическое строение.
находится внутри запрещенной зоны (рис.5.17), то валентная зона заполнена полностью, а верхняя так же, как и в предыдущем случае, полностью свободна. При наложении электрического поля движение электрона невозможно, так как невозможен его переход с уровня на уровень – все уровни энергии заняты. Значит, невозможно возникновение электрического тока в цепи с веществом, имеющим такое электрическое строение.
Таким образом, если нижняя зона заполнена полностью, а верхняя полностью пуста, то кристалл является диэлектриком: движение электронов невозможно из-за отсутствия свободных уровней. Нижняя полностью занятая зона называется валентной, верхняя, полностью свободная, - зоной проводимости.
Чтобы в таких веществах появилось движение электронов, необходима активация электронов – переброс их в свободную (пустую) зону через запрещенный интервал ![]() - это возможно сделать с помощью тепловой энергии. В зависимости от ширины запрещенной зоны зонной структуры, представленной рис.5.17, вещества делятся на диэлектрики и полупроводники. Для диэлектриков
- это возможно сделать с помощью тепловой энергии. В зависимости от ширины запрещенной зоны зонной структуры, представленной рис.5.17, вещества делятся на диэлектрики и полупроводники. Для диэлектриков ![]() эВ и поэтому переброс электронов в пустую верхнюю зону с помощью тепловой энергии не возможен, так как
эВ и поэтому переброс электронов в пустую верхнюю зону с помощью тепловой энергии не возможен, так как ![]() при
при ![]() К. Для полупроводников
К. Для полупроводников ![]() эВ.
эВ.
При ![]() число электронов в зоне проводимости (верхней зоне) увеличивается экспоненциально:
число электронов в зоне проводимости (верхней зоне) увеличивается экспоненциально:
![]() . (5.28)
. (5.28)
Из формулы Друде в виде (5.8) следует, что электропроводность:
![]() . (5.29)
. (5.29)
Тогда электрическое сопротивление:
![]() . (5.30)
. (5.30)
Из (5.29) видно, что ![]() увеличивается с ростом температуры экспоненциально за счет роста концентрации электронов в зоне проводимости. Следует отметить, что в валентной зоне при этом также появляются вакантные места (дырки), которые движутся (переходят с уровня на уровень). Рассмотренный механизм характерен для собственной проводимости полупроводников, таких как германий, селен, кремний.
увеличивается с ростом температуры экспоненциально за счет роста концентрации электронов в зоне проводимости. Следует отметить, что в валентной зоне при этом также появляются вакантные места (дырки), которые движутся (переходят с уровня на уровень). Рассмотренный механизм характерен для собственной проводимости полупроводников, таких как германий, селен, кремний.
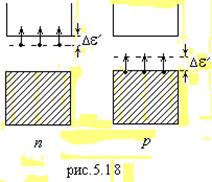
Рассмотрим теперь механизм электропроводности примесных полупроводников. Так, добавление к чистому кремнию всего 0.001 атомного процента фосфора увеличивает электропроводность в 105 раз. Объяснить это можно рассматривая расположение уровней примеси относительно энергетических зон полупроводника. Для примесных полупроводников уровни примесей могут быть расположены у дна зоны проводимости (донорная примесь n) или у вершины валентной зоны (акцепторная примесь p). Ширина запрещенной зоны значительно превышает интервал ![]() (рис.5.18), отделяющий примесный уровень от дна зоны проводимости или верхушки валентной зоны:
(рис.5.18), отделяющий примесный уровень от дна зоны проводимости или верхушки валентной зоны: ![]() , Поэтому вследствие:
, Поэтому вследствие:
![]() (5.29’)
(5.29’)
активация электронов происходит при меньших температурах, чем для собственного полупроводника. Носителями электрического тока являются электроны в зоне проводимости для проводника n–типа и дырки в валентной зоне для проводника p–типа.
 Величина
Величина ![]() для собственного полупроводника,
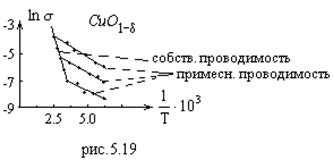
для собственного полупроводника, ![]() - для примесного. На рис.5.19 представлены зависимости электропроводности (в логарифмическом масштабе) от обратной температуры для оксида меди с различным недостатком кислорода (примесный полупроводник)
- для примесного. На рис.5.19 представлены зависимости электропроводности (в логарифмическом масштабе) от обратной температуры для оксида меди с различным недостатком кислорода (примесный полупроводник) ![]() , где
, где ![]() . Видно, что зависимость
. Видно, что зависимость 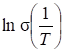 является линейной, как и должно быть по формуле (5.29’). Излом на этой зависимости отделяет области собственной и примесной проводимости. Примесная проводимость имеет меньшую энергию активации (угол между прямой и осью абсцисс уменьшается) и активируется при меньших температурах (больших
является линейной, как и должно быть по формуле (5.29’). Излом на этой зависимости отделяет области собственной и примесной проводимости. Примесная проводимость имеет меньшую энергию активации (угол между прямой и осью абсцисс уменьшается) и активируется при меньших температурах (больших ![]() ), чем собственная проводимость.
), чем собственная проводимость.
Поможем написать любую работу на аналогичную тему

