Рассмотрим процессы, происходящие в цепи при включении (выключении) постоянной ЭДС.
1. ![]() -цепь с
-цепь с ![]() (рис.6.2).
(рис.6.2).
а) Включение ЭДС: ![]() .
.
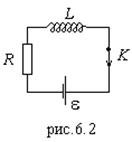 Закон Ома в цепи:
Закон Ома в цепи:
![]() (6.11)
(6.11)
при включении тока (это учтено знаком для ![]() ). Данное уравнение является линейным неоднородным дифференциальным уравнением, решаемым следующим образом. Приведем (6.11) к виду:
). Данное уравнение является линейным неоднородным дифференциальным уравнением, решаемым следующим образом. Приведем (6.11) к виду:
![]() (6.12)
(6.12)
Запишем характеристическое уравнение для данного дифференциального уравнения:
![]()
Решение дифференциального уравнения (6.12) примет вид:
![]() , (6.13)
, (6.13)
где ![]() - константы, определяемые подстановкой решения (6.13) в (6.12) и начальным условием:
- константы, определяемые подстановкой решения (6.13) в (6.12) и начальным условием: ![]() :
:
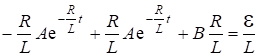 .
.
Отсюда: ![]() . В момент включения
. В момент включения ![]() ток отсутствует
ток отсутствует ![]() , тогда из (6.13) следует, что:
, тогда из (6.13) следует, что: ![]() . Таким образом, с учетом
. Таким образом, с учетом ![]() , окончательно решение уравнения (6.11) имеет вид:
, окончательно решение уравнения (6.11) имеет вид:
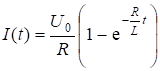 . (6.14)
. (6.14)
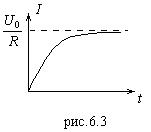
 Графическая временная зависимость тока представлена на рис.6.3. Значение тока
Графическая временная зависимость тока представлена на рис.6.3. Значение тока ![]() соответствует закону Ома для постоянного тока и называется установив-шимся. Величина падения напряжения на катушке индуктивности как функция времени выражается экспоненци-альной зависимостью:
соответствует закону Ома для постоянного тока и называется установив-шимся. Величина падения напряжения на катушке индуктивности как функция времени выражается экспоненци-альной зависимостью:
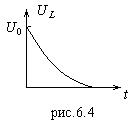
![]() , (6.15)
, (6.15)
приведенной на рис.6.4.
Следующее отношение имеет смысл времени релаксации:
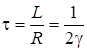 . (6.16)
. (6.16)
Из (6.14) ясно, что при ![]() ток достигает установившегося значения, при этом напряжение на индуктивности
ток достигает установившегося значения, при этом напряжение на индуктивности ![]() .
.
б) Процесс выключения ЭДС будет описываться аналогично, но знак ![]() будет противоположным по действию: она будет поддерживать ток в цепи. Закон Ома в цепи дает уравнение:
будет противоположным по действию: она будет поддерживать ток в цепи. Закон Ома в цепи дает уравнение:
![]() . (6.17)
. (6.17)
В начальный момент времени ток ![]() , а равен установившемуся значению
, а равен установившемуся значению ![]() . Тогда решение (6.13) имеет вид:
. Тогда решение (6.13) имеет вид:
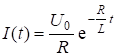 , (6.18)
, (6.18)
и при ![]()
![]() . Напряжение на катушке индуктивности, по-прежнему, определяется как
. Напряжение на катушке индуктивности, по-прежнему, определяется как ![]() и равно:
и равно:
![]() . (6.19).
. (6.19).
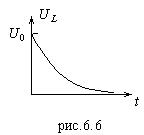
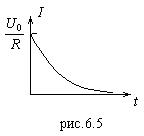 Графические зависимости (6.18) и (6.19) приведены на рис.6.5 и 6.6, соответственно.
Графические зависимости (6.18) и (6.19) приведены на рис.6.5 и 6.6, соответственно.
Видно, что при выключении внешней ЭДС ток в цепи становится равным нулю не мгновенно, а лишь тогда, когда станет равным нулю ![]() (т.е.
(т.е. ![]() )
)
2. ![]() - цепи с
- цепи с ![]() (рис.6.7).
(рис.6.7). ![]() .
.
а) Зарядка конденсатора (включение ключа К).
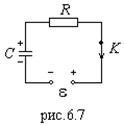 Закон Ома в цепи:
Закон Ома в цепи:
![]() . (6.20)
. (6.20)
Продифференцируем по времени это выражение:
![]() . (6.21)
. (6.21)
Решение ищем в виде ![]() . Для
. Для ![]() ,
, ![]() .
. ![]() . Таким образом:
. Таким образом:
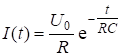 . (6.22)
. (6.22)
 Данная графическая зависимость представлена на рис.6.5. После того, как конденсатор зарядится до
Данная графическая зависимость представлена на рис.6.5. После того, как конденсатор зарядится до ![]() , ток исчезнет (при
, ток исчезнет (при ![]()
![]() ). Следует заметить, что в отличие от тока, заряд на конденсаторе в начальный момент времени равен нулю (отсутствует); он накапливается по мере убывания силы тока и зарядки конденсатора: при
). Следует заметить, что в отличие от тока, заряд на конденсаторе в начальный момент времени равен нулю (отсутствует); он накапливается по мере убывания силы тока и зарядки конденсатора: при ![]() , и из (6.20)
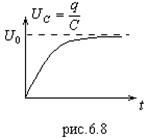
, и из (6.20) ![]() . Закон изменения напряжения на конденсаторе имеет вид, приведенный на рис.6.8, соответствующий аналитической зависимости, полученной при интегрировании (6.22):
. Закон изменения напряжения на конденсаторе имеет вид, приведенный на рис.6.8, соответствующий аналитической зависимости, полученной при интегрировании (6.22):
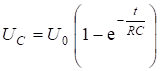 .
.
б) Короткое замыкание в ![]() - цепи.
- цепи.
При отключении ЭДС из цепи, т.е. закорачивании ее и сохранении цепи замкнутой, по цепи пойдет ток с начальным значением ![]() , который по направлению противоположен предыдущему. Будет наблюдаться разрядка конденсатора. Закон уменьшения тока в данном случае совпадает с (6.22) и рис.6.5, а падение напряжения на конденсаторе происходит так же, как на катушке индуктивности при отключении постоянной ЭДС (рис.6.6).
, который по направлению противоположен предыдущему. Будет наблюдаться разрядка конденсатора. Закон уменьшения тока в данном случае совпадает с (6.22) и рис.6.5, а падение напряжения на конденсаторе происходит так же, как на катушке индуктивности при отключении постоянной ЭДС (рис.6.6).
3. ![]() - цепь с
- цепь с ![]() (рис.6.9).
(рис.6.9). ![]() .
.
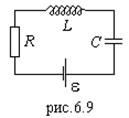 Закон Ома в цепи:
Закон Ома в цепи:
![]() . (6.23)
. (6.23)
Подставим в (6.23): ![]() и запишем его для переменной
и запишем его для переменной ![]() :
:
![]() . (6.24)
. (6.24)
Продифференцировав по времени выражение (6.24), получим:
![]() (6.25)
(6.25)
или в приведенном виде:
![]() , (6.26)
, (6.26)
где ![]() ;
; ![]() . Характеристическое уравнение:
. Характеристическое уравнение:
![]() .
.
Корнями этого уравнения являются:
![]() , где
, где ![]() . (6.27)
. (6.27)
Для однородного дифференциального уравнения решение запишется в виде:
![]() . (6.28)
. (6.28)
 Из начального условия
Из начального условия ![]()
![]() получаем:
получаем:![]() . Окончательно, с учетом формул Эйлера
. Окончательно, с учетом формул Эйлера
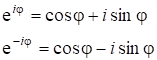
получим:
![]() . (6.29)
. (6.29)
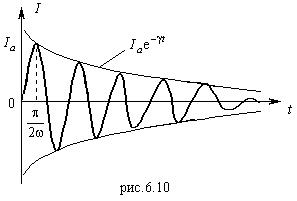
Зависимость (6.29) представлена на рис.6.10. Для
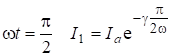 .
.
Видно, что ![]() - затухающая функция. Амплитуда колебаний изменяется по закону:
- затухающая функция. Амплитуда колебаний изменяется по закону: ![]() . Период затухания колебаний:
. Период затухания колебаний:
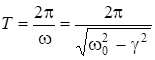 . (6.30)
. (6.30)
Найдем ![]() по формуле:
по формуле: ![]() :
:
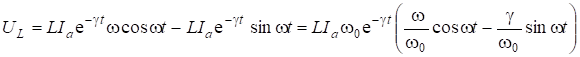
Введем обозначения: 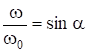 ;
; 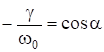 .
.
Для ![]()
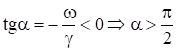 . Обычно
. Обычно ![]() , тогда
, тогда ![]() .
.
Используя формулы приведения, получим выражение для ![]() в форме:
в форме:
![]() .
.
Амплитуду ![]() найдем из начального условия:
найдем из начального условия: ![]() . Отсюда:
. Отсюда: ![]() . Таким образом, окончательное выражение для
. Таким образом, окончательное выражение для ![]() примет вид:
примет вид:
![]() . (6.31)
. (6.31)
Используем метод векторных диаграмм, чтобы проиллюстрировать полученный результат. Гармонически изменяющаяся величина может быть представлена вектором, длина которого равна амплитуде, а угол между вектором и выбранной осью – фазе. Из диаграммы рис.6.11 видно, что ![]() опережает ток
опережает ток ![]() на угол
на угол ![]() .
.
В случае отсутствия сопротивления в цепи ![]() (нет затухания колебаний).
(нет затухания колебаний).
Найдем ![]() по формуле:
по формуле: ![]() . Тогда:
. Тогда:
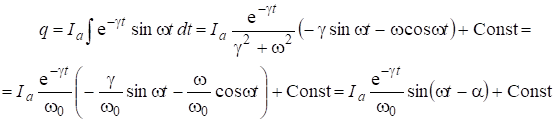 (6.32)
(6.32)
При выводе была использована формула:
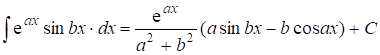 .
.
Для нахождения постоянной используем граничные условия: ![]() (конденсатор разряжен):
(конденсатор разряжен):
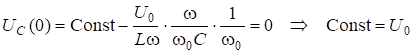 .
.
 Таким образом, напряжение на конденсаторе в любой произвольный момент времени определяется как:
Таким образом, напряжение на конденсаторе в любой произвольный момент времени определяется как:
![]() . (6.33)
. (6.33)
Ясно, что величина ![]() колеблется вокруг значения
колеблется вокруг значения ![]() . При
. При ![]() : конденсатор заряжается до
: конденсатор заряжается до ![]() и ток в цепи прекращается:
и ток в цепи прекращается:
![]() .
.
При этом величина напряжения на катушке индуктивности также стремится к нулю:
![]() .
.
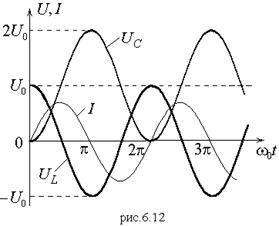
Графики зависимости ![]() для случая
для случая ![]() (
(![]() ) приведены на рис.6.12. Легко проверить, что в любой момент времени выполняется:
) приведены на рис.6.12. Легко проверить, что в любой момент времени выполняется: ![]() . Максимально возможное значение напряжения на конденсаторе
. Максимально возможное значение напряжения на конденсаторе ![]() . Если
. Если ![]() . Это необходимо учитывать при подборе конденсатора, чтобы не возникло пробоя.
. Это необходимо учитывать при подборе конденсатора, чтобы не возникло пробоя.
При увеличении ![]() характер колебаний тока и напряжения в цепи изменяется. При
характер колебаний тока и напряжения в цепи изменяется. При ![]() ,
, ![]() и колебания становятся апериодическими. При этом омическое сопротивление в цепи называется критическим:
и колебания становятся апериодическими. При этом омическое сопротивление в цепи называется критическим:
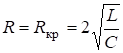 . (6.34)
. (6.34)
Уравнение колебаний при ![]() также имеет вид (6.26):
также имеет вид (6.26):
![]()
которому соответствует характеристическое уравнение:
![]() .
.
Кратными корнями его являются:
![]() . (6.35)
. (6.35)
Решение однородного дифференциального уравнения в случае кратных корней имеет вид:
![]() . (6.36)
. (6.36)
Из начального условия ![]() получаем:
получаем:![]() . Тогда:
. Тогда:
![]() . (6.37)
. (6.37)
Найдем: ![]() .
.
Используем начальное условие:
![]()
Таким образом:
![]() . (6.38)
. (6.38)
![]() . (6.39)
. (6.39)
Найдем напряжение на конденсаторе:
![]() . (6.40)
. (6.40)
К (6.40) применим интегрирование по частям:
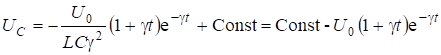 .
.
Используем начальное условие:
![]() .
.
Окончательно получаем:
![]() . (6.41)
. (6.41)
Найдем максимальное значение силы тока:
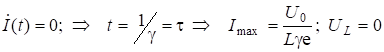 .
.
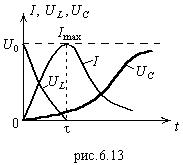 При
При ![]() . Все приведенные зависимости изображены на рис.6.13. Видно, что когда конденсатор заряжается до
. Все приведенные зависимости изображены на рис.6.13. Видно, что когда конденсатор заряжается до ![]() , ток в цепи прекращается.
, ток в цепи прекращается.
Введем величину добротности контура:
![]() . (6.42)
. (6.42)
Здесь ![]() - энергия, запасенная в контуре;
- энергия, запасенная в контуре; ![]() ‑ уменьшение энергии за период
‑ уменьшение энергии за период
Поможем написать любую работу на аналогичную тему

