Рассмотрим 
- цепь с переменной ЭДС (рис.6.1). Уравнение колебательного контура:
. (6.44)
, (6.45)
где 
При решении уравнения удобно пользоваться комплексной формой записи гармонически изменяющейся величины:
. (6.46)
Сила тока также изменяется со временем по закону:
, (6.47)
где 
- комплексная величина, в которой учитывается разность фаз между 
и 
.
Ставится задача: найти амплитудные и фазовые соотношения между током и напряжением в цепи.
Перепишем уравнение (6.45) в виде:
. (6.48)
Из (6.47) и (6.46): 
. Подставим эти выражения в (6.48):
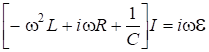. (6.49)
Разделим обе части на 
и учтем, что 
. Тогда при:
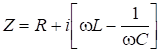(6.50)
уравнение примет вид закона Ома:
. (6.51)
Здесь 
- импеданс. Для переменного тока импеданс играет роль сопротивления, но из-за комплексности он позволяет учесть не только соотношения между амплитудами, но и между фазами тока и напряжений.
Для того чтобы найти соотношения между амплитудами, возьмем модули от обеих частей закона Ома (6.51):
, (6.52)
где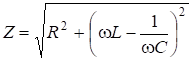 
. Из (6.52) получим амплитуду:
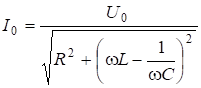. (6.53)
Это закон Ома в вещественной форме; 
- омическое сопротивление; 
- индуктивное сопротивление, а 
- емкостное.
Для определения соотношения между фазами используем метод векторных диаграмм.
Представим комплексное число вектором на комплексной плоскости. Гармонически изменяющаяся величина изображается вектором, длина которого равна амплитуде, а угол между вектором и вещественной осью – фазой.
Из уравнения колебаний (6.49) при : 
, получим:
.
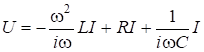Тогда:
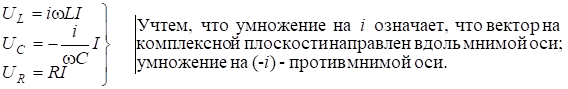
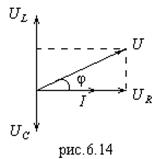Изобразим результаты на векторной диаграмме (рис.6.14). За начало отсчета возьмем 
и направим его вдоль вещественной оси. Так же направлен и вектор тока (по фазе напряжение на сопротивлении совпадает с током). Теперь построим векторы 
, учитывая, что 
направлен вдоль мнимой оси, т.е. вверх, а 
- против мнимой оси, т.е. вниз. После этого сложим векторно 
и получим 
- приложенное напряжение. Из диаграммы рис.6.14 видно, что:
а) опережает на 
.
б) отстает от на .
в) опережает на 
.
Длины векторов 
- это амплитудные значения напряжений.
.
Тогда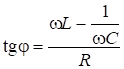 
. Отсюда видно, что при 
, или 
, 
, т.е. опережает по фазе и .
Таким образом, (6.47) можно записать в виде:
.
Знак 
определяется соотношением 
или 
, соответственно: и 
.
К переменным токам без всякого изменения применимы первое и второе правила Кирхгофа с учетом комплексной записи закона Ома (6.51):
1) в каждом узле: 
;
2) для всякого замкнутого контура: 
.
При последовательном соединении импедансов: 
;
при параллельном соединении импедансов: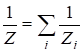 
.
Величина, обратная импедансу, называется проводимостью: 
.
Поэтому при параллельном соединении: 
.
Поможем написать любую работу на аналогичную тему