Резонанс напряжений.
Рассмотрим 
- цепь с элементами, включенными последовательно (рис.6.1). Векторная диаграмма тока и напряжений такой цепи приведена на рис.6.14, откуда:
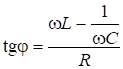
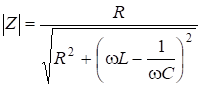; (6.60)
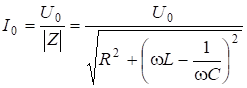. (6.61)
Из диаграммы рис.6.14 и формулы (6.61) видно, что при 
, 
; 
; 
. При таком условии получено максимальное значение тока, что эквивалентно условию:
. (6.62)
При этом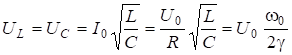 
, т.е. 
, где 
- добротность контура (6.43); при малом затухании 
: 
, т.е. при резонансе 
и в раз больше, чем 
.
Исследуем зависимости 
. Для этого преобразуем формулы следующим образом. Ток в цепи:
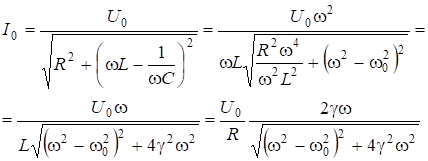(6.63)
Напряжение на элементах цепи:
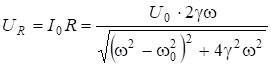; (6.64)
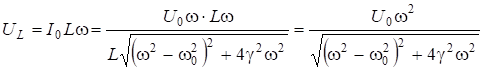; (6.65)
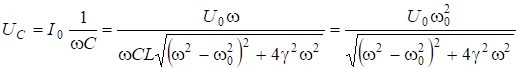. (6.66)
Зависимость угла 
- разности фаз между 
и - от частоты:
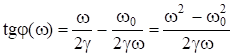. (6.67)
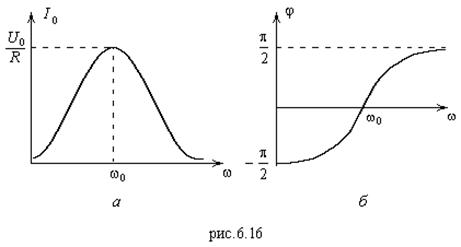
Графические зависимости (6.64) и (6.67) представлены на рис.6.16 (а и б, соответственно).
Достигают ли максимума 
и при каких частотах?
Условие 
отвечает минимуму знаменателя (6.66).
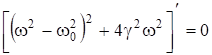. (6.68)
Продифференцировав, получаем: 
, откуда:
или:
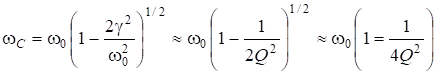. (6.69)
Максимальное значение 
при этом:
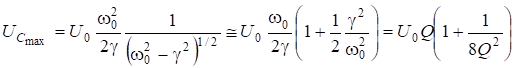. (6.70)
При совпадении частоты вынужденных колебаний и собственной частоты наблюдается резонанс: 
.
 |
При
Найдем условие максимума 
.
.
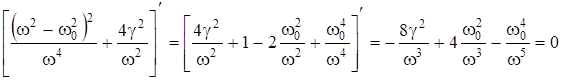Упростим: 
, откуда:
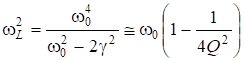. (6.71)
Значение при этом:
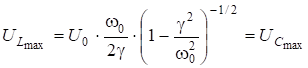. (6.72)
При 
.
При 
Таким образом, 
достигают максимума при частотах, не равных 
. Оценим, насколько велико это отличие. Так, при 
: 
; 
.
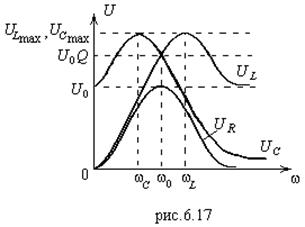Графики частотной зависимости (6.64), (6.65) и (6.66) приведены на рис.6.17. Из графиков видно, что если выходным сигналом является , то контур служит для ослабления высоких частот (высокочастотный фильтр –ВЧ-фильтр). Если же на выходе снимается , то ослабляется низкочастотная часть, и контур служит низкочастотным фильтром (НЧ-фильтром).
Оценим отличие 
по (6.69) и (6.71).
Для 
. Следовательно, при большой добротности, т.е. при малом затухании, можно считать, что максимумы 
совпадают по частоте. Величины максимумов 
в раз больше, чем 
.
Поможем написать любую работу на аналогичную тему