Уравнения Максвелла необходимо дополнить соотношениями, выражающими закон сохранения энергии.
При изменении электромагнитного поля в среде и прохождении через нее электрического тока в единице объема среды совершается элементарная внешняя работа:
![]() .
.
Формула получена из (7.16) с учетом закона Джоуля-Ленца (5.9). Если ![]() - внутренняя энергия единицы объема среды, то:
- внутренняя энергия единицы объема среды, то:
![]() ;
;
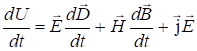 . (7.17)
. (7.17)
Первые два слагаемых – электромагнитная часть плотности энергии, третье - тепловая часть (джоулево тепло). Преобразуем (7.17) к виду:
![]() . (7.18)
. (7.18)
Используя (7.11) и (7.12), имеем с учетом формул (7) Приложения:
![]() , (7.19)
, (7.19)
где ![]() - оператор набла (1.18). Введем обозначение:
- оператор набла (1.18). Введем обозначение:
![]() . (7.20)
. (7.20)
Тогда:
![]() или
или ![]() (7.21)
(7.21)
В интегральной форме уравнение (7.21) имеет вид:
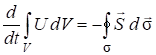 . (7.22)
. (7.22)
Вектор ![]() называется вектором Умова-Пойнтинга (1874 г., 1884 г.).
называется вектором Умова-Пойнтинга (1874 г., 1884 г.).
![]() - это поток вектора
- это поток вектора ![]() сквозь замкнутую поверхность
сквозь замкнутую поверхность ![]() . Знак “‑“ показывает, что
. Знак “‑“ показывает, что ![]() и
и ![]() разнонаправлены, если поток положителен.
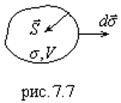
разнонаправлены, если поток положителен. ![]() - это электромагнитная энергия объема, заключенного внутри замкнутой поверхности
- это электромагнитная энергия объема, заключенного внутри замкнутой поверхности ![]() (см.рис.7.7).
(см.рис.7.7).
Тогда, вектор Умова-Пойнтинга определяет энергию электромагнитного поля, пересекающую в единицу времени площадку единичной площади, перпендикулярную направлению распространения этой энергии.
Размерность вектора ![]() - Вт/м2.
- Вт/м2.
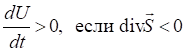 , т.е. энергия в объеме увеличивается за счет потока вектора
, т.е. энергия в объеме увеличивается за счет потока вектора ![]() внутрь поверхности.
внутрь поверхности.
Поможем написать любую работу на аналогичную тему

