Простейшей системой, излучающей электромагнитные волны, является точечный диполь, дипольный момент которого изменяется во времени по гармоническому закону. Такой диполь называется вибратором Герца. Он представляет собой два шара периодически заряжающихся и разряжающихся через соединяющий их проводник. Задача об излучении диполя Герца в теории излучающих систем имеет существенное значение.
В сферической системе координат компоненты ![]() по результатам расчета следующие:
по результатам расчета следующие:
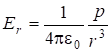 ;
; 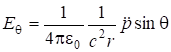 ;
; ![]() . (7.66)
. (7.66)
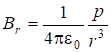 ;
; 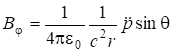 ;
; ![]() . (7.67)
. (7.67)
 Для волновой зоны
Для волновой зоны ![]() :
: ![]() , поэтому в (7.66)
, поэтому в (7.66) ![]() . Аналогично и для вектора магнитной индукции; при
. Аналогично и для вектора магнитной индукции; при ![]() в (7.67)
в (7.67) ![]() . Направления для
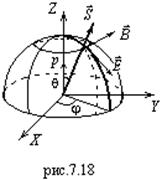
. Направления для ![]() показаны на рис.7.18. Здесь
показаны на рис.7.18. Здесь ![]() - дипольный момент. Вектор
- дипольный момент. Вектор ![]() направлен по касательной к меридианальной плоскости,
направлен по касательной к меридианальной плоскости, ![]() - к горизонтальной. Тогда
- к горизонтальной. Тогда ![]() направлен вдоль радиуса - вектора
направлен вдоль радиуса - вектора ![]() , при этом изменение направления вектора
, при этом изменение направления вектора ![]() не изменит направления
не изменит направления ![]() . При
. При
![]() ;
; ![]() .
.
Мгновенная мощность излучения.
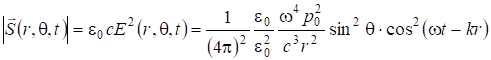 . (7.68)
. (7.68)
Средняя мощность:
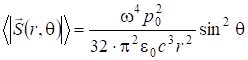 . (7.69)
. (7.69)
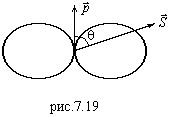 Полярная диаграмма распределения средней мощности в зависимости от направления излучения диполя приведена на рис.7.19. Зависимость
Полярная диаграмма распределения средней мощности в зависимости от направления излучения диполя приведена на рис.7.19. Зависимость ![]() от направления выражается множителем
от направления выражается множителем ![]() . Мощность
. Мощность ![]() максимальна при
максимальна при ![]() , т.е. перпендикулярно оси диполя. Вдоль оси диполя
, т.е. перпендикулярно оси диполя. Вдоль оси диполя ![]() энергия не излучается.
энергия не излучается.
Полная энергия, излучаемая диполем за одну секунду по всем направлениям, может быть рассчитана, если найти поток ![]() через поверхность сферы радиусом
через поверхность сферы радиусом ![]() с центром в осцилляторе.
с центром в осцилляторе.
Разобьем сферу на кольца с азимутом ![]() и шириной
и шириной ![]() . Площадь кольца
. Площадь кольца ![]() , и значения
, и значения ![]() во всех точках кольца одинаковы. Поэтому:
во всех точках кольца одинаковы. Поэтому:
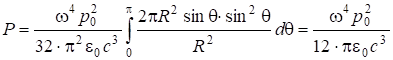 . (7.70)
. (7.70)
Видно, что общий поток излучения не зависит от ![]() , но поток через единичную площадку обратно пропорционален
, но поток через единичную площадку обратно пропорционален ![]() , т.е. уменьшается пропорционально росту общей площади, по которой распределяется излучение. Пропорциональность полной энергии
, т.е. уменьшается пропорционально росту общей площади, по которой распределяется излучение. Пропорциональность полной энергии ![]() носит название “закона голубого неба”, так как голубой цвет имеет наибольшую интенсивность при колебании осцилляторов ионосферы.
носит название “закона голубого неба”, так как голубой цвет имеет наибольшую интенсивность при колебании осцилляторов ионосферы.
На опыте электромагнитные волны впервые были получены Герцем в 1887-88гг. Вибратор Герца представлял собой два металлических шарика, соединенных проводником. Если шарикам сообщить равные, но противоположные по знаку, заряды и предоставить систему самой себе, то будет происходить колебательный процесс перезарядки шаров. На расстоянии ![]() система может рассматриваться как диполь, момент которого изменяется со временем.
система может рассматриваться как диполь, момент которого изменяется со временем.
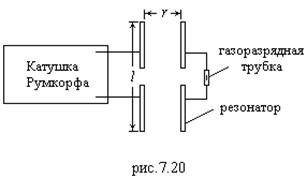 Катушка Румкорфа (высокочастотный трансформатор) – заряжает стержни диполя до тех пор, пока в промежутке между ними не проскакивает искра (разряд). В это время вибратор излучает волну
Катушка Румкорфа (высокочастотный трансформатор) – заряжает стержни диполя до тех пор, пока в промежутке между ними не проскакивает искра (разряд). В это время вибратор излучает волну![]() . Вибратор Герца имел длину 2.5м¸1м,
. Вибратор Герца имел длину 2.5м¸1м, ![]() . Лебедев (1885г.) создал вибратор с
. Лебедев (1885г.) создал вибратор с ![]() . Фиксируется волна резонатором. Простейший резонатор представляет таких же два металлических стержня, соединенных газоразрядной трубкой. Расстояние до резонатора r>>l. Блок– схема показана на рис.7.20.
. Фиксируется волна резонатором. Простейший резонатор представляет таких же два металлических стержня, соединенных газоразрядной трубкой. Расстояние до резонатора r>>l. Блок– схема показана на рис.7.20.
Дипольный момент может возникнуть также при движении постоянного заряда ![]() :
:
![]() ,
,
где ![]() - изменяющееся во времени положение заряда. Сказанное можно пояснить, предположив, что в начале отсчета находится неподвижный заряд ‑
- изменяющееся во времени положение заряда. Сказанное можно пояснить, предположив, что в начале отсчета находится неподвижный заряд ‑![]() . Получится пара зарядов с изменяющимся по времени расстоянием между ними.
. Получится пара зарядов с изменяющимся по времени расстоянием между ними.
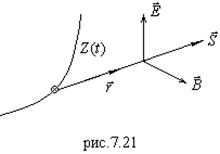 Далее воспользуемся формулами (7.66) и (7.67) для
Далее воспользуемся формулами (7.66) и (7.67) для ![]() и
и ![]() . Так как
. Так как ![]() ,
, ![]() , то полученная электромагнитная волна является сферической, и вектор
, то полученная электромагнитная волна является сферической, и вектор ![]() направлен по радиусу (см.рис.7.21). Найдем
направлен по радиусу (см.рис.7.21). Найдем ![]() .
.
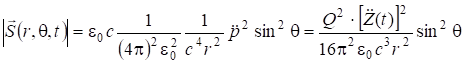 . (7.71)
. (7.71)
Полная энергия излучения:
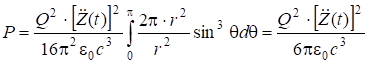 . (7.72)
. (7.72)
Видно, что мощность излучается только тогда, когда заряд движется с ускорением. Равномерно движущийся заряд не излучает.
Осциллятор совершает незатухающие колебания лишь в случае, если они поддерживаются каким-либо внешним источником. Без такого источника колебания будут затухать даже при движении в свободном пространстве, так как осциллятор теряет энергию на излучение (радиационное затухание).
Поможем написать любую работу на аналогичную тему

