Мы знаем, что в электрическом поле объёмная плотность энергии равна:
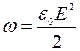
Преобразуем это выражение 
Преобразуем это выражение и подставим в выражение для напряжённости электрического поля:
А так как
Получаем
Возьмём интеграл по всему пространству(охватив всё) получаем:
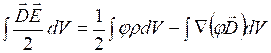
Поскольку 
~
, 
~
~
, 
~
, то на границе поверхности и выражение для энергии поля принимает вид
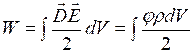- это другое выражение для энергии, здесь уже входит заряд, то есть носителем энергии является заряд. Преобразуем правую часть: 
. Для простоты перейдём от объёмного заряда к точечному. - потенциал создаваемый всеми зарядами кроме 
в этой точке.
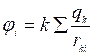- потенциал создаваемый k-тым зарядом в той точке, где находится i-тый заряд.
- расстояние между зарядами i и k.
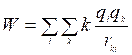- энергия всех зарядов системы.
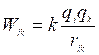- для одной пары зарядов.
- учитывает одну и туже величину дважды, отсюда
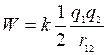-энергия взаимодействия двух зарядов.
Если у нас три заряда, энергию можно посчитать, как энергию взаимодействия первого со вторым, первого с третьим и второго с третьим.
r и k не ноль. Обратим внимание на энергию найденную тремя способами: через заряд, через и через 
. Если рассматривать точечный заряд в отдельности, то собственная его энергия, энергия взаимодействия элементов заряда между собой, то выражение для энергии двух зарядов не содержит собственные энергии самих зарядов, а лишь энергию их взаимодействия между собой. В отличии от формул содержащих выражение для полей и непрерывно распределённых зарядов. Последние уже содержат собственную энергию бесконечна. Выражение не содержит собственной энергии.
Поможем написать любую работу на аналогичную тему