Если у нас имеются стационарные электромагнитное поле – поле которые не меняются со временем: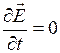 
и 
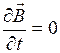, то система уравнений для стационарного магнитного поля принимает вид
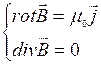
Первое из этих уравнений утверждает, что в точке, где есть j - возникает вихревое магнитное поле. Второе уравнение свидетельствует об отсутствии магнитных зарядов.
Представим эти уравнения в другом виде, из второго уравнения следует, что B можно представить в виде:
, так как 
Вектор А носит название векторного потенциала. Но это определение не однозначно. Если вместо 
ввести 
, где 
- некоторый скалярная функция, то
Вектор А задаётся с точностью до grad некоторой скалярной функции. Подставим выражение для вектор B в первое из уравнений для стационарного магнитного поля. И пользуясь уравнениями векторного анализа, получим
Из произвола задания вектора 
можно выбрать такой вектор, при котором дивергенция вектора F равняется 0. Тогда система уравнений для стационарного поля запишется в следующем виде.
Выберем 
, тогда получаем следующую систему:
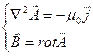
Задача нахождения выражения для В сводится к решению уравнения Пуассона для А. Уравнение Пуассона мв решали раньше, поэтому напишем сразу его решение
Данная система является эквивалентной исходной системе.
- уравнение Пуассона для данной задачи. Найдём вид решения для магнитного поля В.
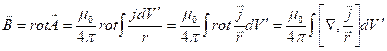
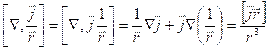
(j=const) – так как имеет дело с постоянным током.
На практике часто имеют дело с линейными токами. Для того, что бы перейти к линейному току, заменим:
.
Отсюда магнитное поле
Для линейных токов:
Магнитное поле от элемента тока на расстоянии dl от него будет равняться
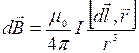- магнитное поле элемента тока 
.
Поможем написать любую работу на аналогичную тему