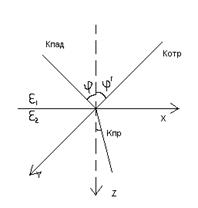
Пусть плоская волна падает на границу двух сред ε1 и ε2. Отражается под углом падает φ и отражается под углом φ’, преломляется под углом ψ.
Вектор напряжённости для ЭМВ меняется со временем и пространственно по закону 
.
Как мы знаем, на границе раздела двух сред тангенсальное слагающее вектора 
не испытывает скачка. Запишем это условие ниже(на графике отметить к). Мы учли, что в первой среде в точке касания с границей раздела имеется падающая и отражённая волна, а во второй среде только преломлённая.
|
Подставим в это уравнение
,
чтоб это условие не зависело от времени, необходимо, чтобы: 
В этом случае iωt сократится. Это условие означает, что при отражении и преломлении частота излучения не меняется. Тогда граничные условия будут выглядеть: 
или 
Уравнение на границе раздела двух сред z=0, из-за независимости выбора x и y следует 
и 
. В это случае в любой точке на поверхности будет иметь место условие . Если считать, что ось y перпендикулярна плоскости падения, то 
Луч падающий, луч отражённый, перпендикуляр проведённый к поверхности в точку падения лежат в одной плоскости!
Из второго условия для x-ой компоненты k, получаем 
, но так как 
.
Так как луч падающий и отражённый лежат в одной среде и частота при отражении не меняется, то 
. А следовательно 
, а следовательно 
, следовательно 
и 
- это закон отражения. Угол отражения равняется углу падения. Соответственно для х-ой составляющей:
, а так как 
n – абсолютный показатель преломления.
Мы получили, что электромагнитная волна на границе двух сред на границе двух сред подчиняются законам геометрической оптики. А если учесть, что c=3*108мc, мы видим, что свет есть электромагнитная волна.
С помощью уравнений Максвелла можно найти закон Малюса, Брюстера, коэффициент отражения стекла и многое другое!
Поможем написать любую работу на аналогичную тему