Постоянные электромагнитные поля.

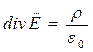Рассмотрим случаи, когда Е и В со временем не меняются – такие поля называются стационарными. В этом случае: . Тогда уравнения Максвелла в котором  и , вообщем-то перемешаны, распадаются на две независимые системы. Только для магнитного поля  и  . и только для электрического   и 

Электрические и магнитные явления становятся независимы.

 Рассмотрим случай стационарного электрического поля, в этом случае поле будет статическое.

Рассмотрим первое уравнение для этого поля 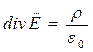. Умножим на dV и возьмём интеграл по объёму. Оно показывает, что истоком электрического поля является заряд, и в интегральной форме оно будет записываться следующим образом: . Здесь S – произвольная замкнутая поверхность, V – объём ограниченный этой поверхностью.

СМЫСЛ: Поток вектора Е через произвольную замкнутую поверхность равен суммарному электрическому заряду, который расположен внутри этой поверхности.

Теперь рассмотрим второе уравнения для постоянного электрического поля. Запишем его в интегральной форме . Далее применим теорему Стокса, получим:  Циркуляция Е по произвольному замкнутому контуру равняется нулю.

                            две точки (1 и 2). Тогда получаем, что интеграл по

                            замкнутому контуру равен сумме интегралов из 1 в 2

                            по пути А и из 2 в 1 по пути В.

                Тогда получаем следующее выражение:

. Теперь поменяем пределы интегрирования, а следовательно, поменяется и знак: . Теперь перенесем одно из слагаемых вправо . Смысл некоторых выражений:

Е – является характеристикой поля;

 - работа перемещения единицы положительного заряда из 1 в 2 точку.

В электростатическом поле работа по перемещению единицы положительного заряда из  одной точки в другую не зависит от пути этого перемещения.

Это будет тогда, когда  (под интегралом будет полным дифференциал). Тогда  разность потенциалов. Мы видим, что работа перемещения заряда из одной точки в другую не зависит от пути интегрирования, а зависит от значения некоторой функции φ в 1 и 2 точке. Эта функция является скалярной характеристикой поля и носит название потенциала. Мы определили разность потенциалов. Но если положить какой-нибудь из потенциалов например φ2=0, то φ1 будет определять потенциал поля в данной точке. В электростатическом поле можно задать в каждой точке потенциал. Такие поля носят название потенциальных – поля для которых в каждой точке можно задать потенциал.

Электростатическое поле – это потенциальное поле, то есть везде можно задать потенциал.

Если известно поле , то можно определить разность потенциалов, или можно и наоборот, зная потенциал в каждой точке пространства можно определить напряжённость в каждой точке пространства: . А так как если l выбирать вдоль осей (x,y,z,), то вектор E=-grad φ. Оперировать с потенциалом поля проще  - его потенциал является скалярной величиной. Найдём уравнение для потенциала и его решение.