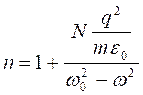Поляризация в быстро переменных полях (дисперсия).

Рассмотрим поляризацию диэлектриков помещённое в электромагнитное поле, в котором электрический вектор меняется по закону . Как и в случае поляризации без дипольных молекул (атомов) под действием электрического поля электроны будут смещаться, создавая индуцированный дипольный момент , как и ранее вектор поляризации будет равняться . И вся задача сводится к нахождению смещения электрона под действием ЭП r/ запишем основное

Запишем уравнение движения:

 - 2-ой закон Ньютона,

, где - сила радиационного трения.

 - постоянная Гука.

Известно, что смещение по закону Гука приводит к гармоническому колебанию с частотой . В этом случае заряды движутся ускоренно, а ускоренные заряды непременно должны излучать электромагнитные волны, а следовательно, должно происходить затухание. Поэтому чисто формально введем ещё один член, зависящий от ускорения движения электрона, который носит название силы радиационного трения и приводит к затуханию колебания

Итак, решим это уравнение и найдём r из него.

, (при малых колебаниях). Подставим всё в выше стоящее уравнение и получим: , где  - собственные колебания электрона.

Будем рассматривать установившиеся колебание, то есть , так как под действием внешних сил устанавливается вынужденное колебание и смещение меняется по тому же закону.

, где =r. Получим 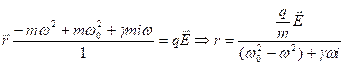. В этом процессе могут участвовать не только электроны, но и ионы, у которых различные массы, знак заряда и его величина.

Подставим в формулу (1), а также умножим на :

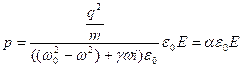, где 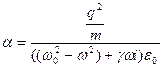 поляризуемость одной молекулы., где P-вектор поляризации, а -дипольный момент.

. Соберём всё в одну формулу, умножив на  (на комплексно сопряжённое) - диэлектрическую проницаемость, получим:

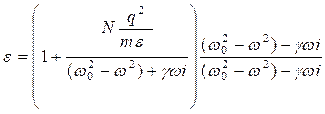
Получим: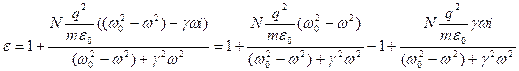

Для простоты воспользуемся тем, что концентрация небольшая.

,

Примет вид

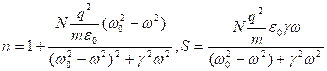
Рассмотрим случай, когда , то есть когда , тогда

Тогда

Если рассматривать случай, когда , то получим, что

Но если не пренебрегать ,то график будет выглядеть следующим образом.

1,3 – нормальная дисперсия 2 – аномальная дисперсия

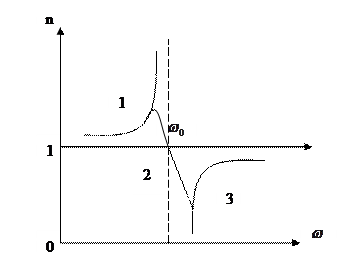Рассмотрим смысл мнимой составляющей в н. Комплексная составляющая в показателе преломления, которой нельзя пренебрегать в случае если . Запишем выражение для электрического вектора ЭМВ.

, . Следовательно: 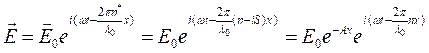, где .

n

Волна затухающая вблизи  к . S будет максимальна и амплитуда волны будет максимальной. Когда частота света приближается к частоте собственных колебаний, то происходит интенсивное поглощение, и в спектре в этом месте будет темнота (т.е. аномальная область).

В этом случае н комплексный н* следовательно н

S действительная часть показателя комплексного преломления.  Мы видим, что А - даёт нам затухающую часть, а второй незатухающую часть. то есть имеет место поглощение ЭМВ.

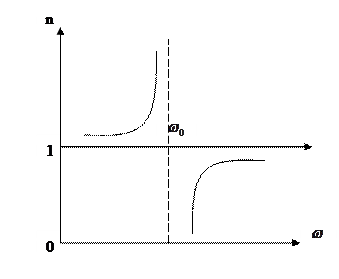
В целом, показатель преломления растет с частотой, но в малых областях частот, вблизи собственных частот колебаний  наблюдается сильное поглощение электромагнитных волн и дисперсионная кривая убывает с частотой и в области поглощения эта дисперсия носит название аномальной. и кривая будет иметь такой вид.

Теперь рассмотрим случай с плазмой. Рассмотрим, когда свободный электроны и ионы. w0=0.

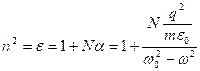
в случае распространения ЭМВ в плазме мы видим что когда  действительный показатель преломления и мнимый если наоборот и волна не проходит через плазму.

Так как это плазма и заряды никак не связанны, то запишем без затухания, то есть . 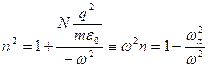, где частота Ленгмюра или плазменная частота. Если ,следовательно (электроны и ионы).

Здесь мы имеем случай, когда вещество находится в ионизированном состоянии (плазменном).