Запишем первое уравнение Максвелла ![]() (
(![]() =1).
=1). ![]() . Подставляя в уравнение Максвелла, получаем
. Подставляя в уравнение Максвелла, получаем ![]() .
.
Решением этого уравнения является ![]()
Соответственно для диэлектрика получаем ![]() , где
, где ![]() ,(k-волновое число).
,(k-волновое число).
![]()
Мы знаем, что![]() , где
, где ![]() - проводимость.
- проводимость.
![]() . Для диэлектриков у нас
. Для диэлектриков у нас ![]() . Следовательно
. Следовательно
![]()
В пустоте ε=1, µ=1 и ![]()
В проводнике ![]() , а следовательно
, а следовательно 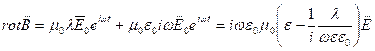
Обозначим ![]() , получаем, что для диэлектриков
, получаем, что для диэлектриков ![]() , а для проводников:
, а для проводников: ![]() .
.
Для проводника уравнение Максвелла имеет такой же вид, что и для диэлектрика, только заменяется ![]() , поэтому используем все результаты, которые мы получили для диэлектриков.
, поэтому используем все результаты, которые мы получили для диэлектриков.
![]() . Пусть
. Пусть ![]()
С одной стороны: ![]()
С другой стороны: 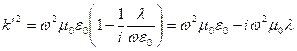
Сравниваем полученные уравнения и получаем, что
![]()
![]() =
=![]()
![]()
Решим эту систему. Если![]() ,
, ![]() , то
, то
![]() или
или ![]() - это выражение для амплитуды волны, которая заходит на глубину x в проводящую среду.
- это выражение для амплитуды волны, которая заходит на глубину x в проводящую среду.
Если sx~1, то ![]()
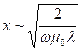 , глубина, на которую может проникнуть электромагнитная волна в проводнике с частотой ω.
, глубина, на которую может проникнуть электромагнитная волна в проводнике с частотой ω.
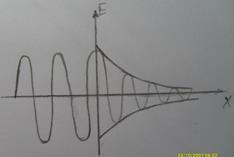
Пример. Пусть у нас имеется волна с частотой ω~1015(частота света), тогда у нас d~10мкм. Получаем, чем больше ω, тем проникновение d уменьшается. А за счёт множителя ![]() -E уменьшается по экспоненциальному закону.
-E уменьшается по экспоненциальному закону.
Поможем написать любую работу на аналогичную тему

