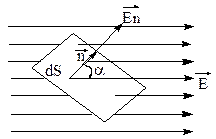|
Рис.1.6. Поток вектора Е через площадку dS. |
Чтобы с помощью силовых линий можно было характеризовать не только направление, но и величину напряженности электростатического поля, их условились проводить с определенной густотой. Число линий напряженности, пронизывающих единицу площади перпендикулярной им поверхности, должно быть равно модулю вектора 
. Число силовых линий, пронизывающих элементарную площадку dS, называется потоком вектора напряженности dФЕ через площадку dS. Эта величина считается по формуле dФЕ=ЕdScos(a), где a - угол между вектором нормали 
к площадке dS и вектором . Представим величину элемента поверхности в виде вектора 
. Таким образом 
- это вектор, численно равный площади элемента поверхности и совпадающий по направлению с наружной нормалью к нему. Тогда Еn=Еcosa - есть проекция вектора на нормаль к площадке dS (рис.1.6) и 
.
Если плоская поверхность S перпендикулярна силовым линиям однородного электрического поля, то поток напряженности через нее равен ФЕ=ЕS. Если площадка dS параллельна линиям напряженности, то поток dФЕ через нее равен нулю, так как в этом случае 
и Еn= 0. Если поверхность S произвольной формы, а поле неоднородное, то поверхность разбивают на малые элементарные площадки dS, на каждой из которых напряженность поля постоянная. Поток напряженности через каждую элементарную площадку равен dФЕ=ЕndS, а поток напряженности поля через всю поверхность представится суммой элементарных потоков и в итоге будет равен 
.
Поток ФЕ может быть положительным и отрицательным в зависимости от угла a, величина которого определяется выбором направления нормали . Для расчета ФЕ через замкнутую поверхность S принято использовать только внешнюю нормаль, т.е. нормаль, направленную наружу от поверхности. Поэтому поток будет считаться отрицательным, если линии напряженности поля направлены внутрь замкнутой поверхности, если линии направлены наружу - он положительный. Единицей измерения потока вектора напряженности электростатического поля является вольт-метр (В×м).
Поможем написать любую работу на аналогичную тему