Будем сообщать уединенному проводнику разные по величине заряды 
При этом проводник будет иметь разные по величине потенциалы 
.Оказывается отношение 
- есть величина постоянная для данного проводника и не зависит от величины сообщенного заряда, а зависит только от геометрической формы проводника и диэлектрической проницаемости окружающей его среды.
Это отношение дает величину электроемкости уединенного проводника, т.е.
C=q/
. (5)
Электрическая емкость измеряется в фарадах: 1Ф= 1Кл / 1В, а также в мФ, мкФ, нФ, пФ ...; причем 1мФ = 10-3 Ф, 1мкФ = 10
Ф, 1 нФ = 
Ф, 1 пФ = 
Ф.
Потенциал заряженного шара радиуса R равен 
, с учетом этого находим емкость уединненого шарового проводника: 
, (6)
т.е. оказывается , что С пропорциональна радиусу шарового проводника R.
Подсчитаем емкость Земного шара, имеющего радиус 
км 
м.
Ф = 700 мкФ.
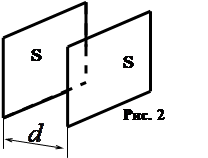Для получения большей емкости используют конденсаторы в виде двух проводников, помещенных близко друг от друга. В этом случае емкость 
. (7)
Для плоского конденсатора, (см. рис. 2), 
тогда по формуле (7) можно найти 
, (8)
где 
– диэлектрическая проницаемость вещества между пластинами.
На электрических схемах электрические конденсаторы обозначают так: a) рис. 3. а - конденсатор постоянной емкости,
б) рис. 3.б- конденсатор переменной емкости,
в) рис. 3. в - подстроечный конденсатор.
|
С1 С2 Сn
 |
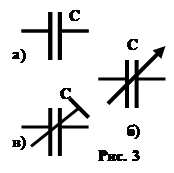
При параллельном соединении конденсаторов, (см. рис. 4) общий заряд qΣ= q1+q2+…+qn.
Используя формулу (7), находим, что UСΣ= UC1+UC2+…+ UCn, откуда СΣ= C1+C2+…+ Cn=ΣCi (9)
При последовательном соединении конденсаторов, (см. рис. 5) UΣ= U1+U2+…+ Un, что согласно (7) можно переписать так 
, откуда 
, (10)
т.е. суммарная емкость уменьшается.
Поможем написать любую работу на аналогичную тему