dФm=B(в)dS(в); Фm=∫B(в)dS(в); Линии индукции магнитного поля замкнуты. Рассмотрим замкнутую повехность S и линию индукции, пронизывающую эту поверхность. Т.к. линия индукции замкнута,
то каждая из них будет пронизываться замкнутой поверхностью
дважды, один раз входя, другой раз выходя. В результате этого она войдет в выражение для потока вектора В через замкнутую поверхность дважды с противоположными знаками. В результате этого суммарный поток вектора магнитной индукции через замкнутую поверхность будет равен нулю, поэтому теорема гаусса для магнитного поля имеет вид:
Замкнутый ∫ dS(в)=0; Эта формула отражает тот факт, что в природе не существует магнитных зарядов, т.е. источника, на котором могли бы начинаться и заканчиваться линии индукции магнитного поля. Магнитный поток через поверхность, ограниченную замкнутым контуром, называется потоком сцепления этого контура ψ. Например потокосцепление рамки и катушки из N витков: ψ=NФ; Ф – магнитный поток через каждый виток.
Потокосцепление контура обусловлена магнитном полем тка в самом контуре называется потокосцеплением самоиндукции. Потокосцепление контура, обусловленное магнитным полем тока в другом контуре, называется потокосцеплением взаимоиндукции.
Закон Ампера. Взаимодействие параллельных токов
Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, равна
![]() . (111.1)
. (111.1)
Направление вектора dF может быть найдено, согласно правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
Модуль силы Ампера вычисляется по формуле
![]() (111.2)
(111.2)
где α — угол между векторами dl и В.
Закон Ампера применяется для определения силы взаимодействия двух токов.
|
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
|
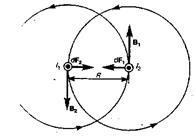
рис.167 |
Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2 (рис. 167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I1 на элемент dl второго проводника с током I2. Ток I1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора В определяется правилом правого винта, его модуль равен
![]()
Направление силы dF1 с которой поле B1
действует на участок dl
второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол ![]() между элементами тока I2 и вектором B1 прямой, равен
между элементами тока I2 и вектором B1 прямой, равен
![]() ;
;
подставляя значение для В1, получим
![]() .
.
Рассуждал аналогично, можно показать, что сила dF2 равна
![]() (111.4)
(111.4)
Сравнение выражений (111.3) и (111,4) показывает, что
![]()
т, е. два параллельных тока одинакового направления притягиваются друг к другу с силой
![]() . (111.5)
. (111.5)
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяем» формулой (111.5).
Поможем написать любую работу на аналогичную тему