Закон Ома в интегральной  и дифференциальной форме

 Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)

Для однородного линейного проводника выразим R через ρ:

ρ – удельное объемное сопротивление; = .

      Найдем связь между  и  в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.

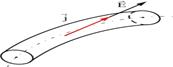
      В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока  и вектор напряженности поля  сонаправлены(рис. 7.6).

: Исходя из закона Ома (7.6.1), имеем

      А мы знаем, что  или . Отсюда можно записать

      это запись закона Ома в дифференциальной форме.

Здесь  – удельная электропроводность.,  Размерность σ – .

      Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость :

.

      Обозначим , тогда ;

Теперь, если удельную электропроводность σ выразить через е, n и b:  то вновь получим выражение закона Ома в дифференциальной форме:

                  -вектор плотности тока

Закон Джоуля Ленца

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля

Математически может быть выражен в следующей форме:

где  — мощность выделения тепла в единице объёма,  — плотность электрического тока,  — напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.