Закон Ома в дифференциальной форме

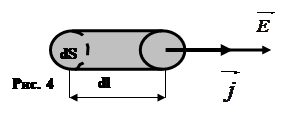
Найдем связь между векторами  и . Для этого мысленно выделим в окрестности некоторой точки проводника элементарный цилиндрический объем с образующими, параллельными векторам  и , (см. рис. 4 ).

Между концами проводника длиной dl напряжение U = Edl, под действием которого через его поперечное сечение площадью dS течет ток I = jdS. Сопротивление цилиндрического проводника, в нашем случае, равно  R =  .Используя закон Ома для участка цепи I = ,  находим: jdS = ,   откуда и получаем закон Ома в дифференциальной форме                        =   =   ,                                            (16)

где  =  удельная электропроводность; = 1 / (Ом м) = 1 См / м, где 1 См = 1 / Ом – это единица измерения электропроводности в СИ, называемая сименс (См). Для металлов согласно классической теории электропроводности    = ,           (17)

где n - концентрация свободных электронов, она может достигать 1010 электрон / м; e – заряд электрона, m – его масса; <  > – средняя длина свободного пробега электрона;                                   < v > =                                                         (18)

< v > – средняя скорость теплового движения электрона, k = 1,38 ×10 Дж/К - постоянная Больцмана. С учетом (18) из (17) следует, что  ~ , а , тогда как опыт показывает, что  ~ Т. Этот и другие недостатки классической теории электропроводности металлов устранила квантовая теория электропроводности.