Принцип Гюйгенса-Френеля.   - Волновая и квантовая оптика. Лекции.

Если свет от источника через сферическое отверстие направить на экран (рис. 3.1 а), то, согласно закону прямолинейного распространения света, на экране должно наблюдаться светлое пятно АВ - изображение отверстия. При уменьшении отверстия его изображение также должно уменьшаться. Однако опыт привел к неожиданному результату: начиная с определенного размера отверстия его дальнейшее уменьшение сопровождается увеличением пятна (А’B’), которое становится расплывчатым, неравномерно освещенным и на нем появляется ряд колец (рис. 3.1 б). Данное явление проникновения световых волн в область геометрической тени, огибания ими препятствий и вообще отклонение их от прямолинейного распространения было названо ди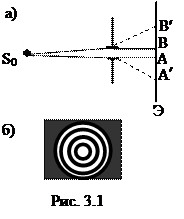фракцией света. Дифракция явилась еще одним подтверждением справедливости волновой теории света.

Изложенный в разделе 2. 1. принцип Гюйгенса помог объяснить дифракцию качественно. Поскольку вторичные источники излучают сферические волны, световое возмущение будет распространяться по всем направлениям. Значит, каждая точка отверстия (рис. 3.1 a) будет источником сферической волны и свет за отверстием может идти по всем направлениям, т.е. отклоняться от прямолинейности. Французский физик О. Френель, развивая идеи Гюйгенса, дал метод количественного расчета дифракции, названный принципом Гюйгенса-Френеля. Рассмотрим основные положения данного принципа:

1. Любой источник света S0 можно заменить эквивалентной системой фиктивных (вторичных) источников, находящихся на какой-либо его волновой поверхности S.

2. Все вторичные источники волновой поверхности S излучают когерентные волны, которые накладываются во всех точках пространства и интерферируют между собой.

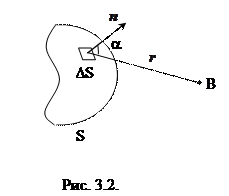
3. Каждый вторичный источник излучает преимущественно в направлении внешней нормали n к dS. Амплитуда вторичной волны в направлении r (где r – расстояние от dS до точки наблюдения В) уменьшается с увеличением угла α между r и нормалью n к dS (рис. 3.2). Она становится равной нулю при α ≥ π/2, т.е. излучение внутрь поверхности не распространяется. От каждого участка dS в точку В приходит световое колебание

.

Здесь Е0 – амплитудное значение светового вектора, С(α)- коэффициент, зависящий от угла α (С(0) = 1, С(π/2)= 0). Тогда результирующий световой вектор от всей волновой поверхности S в точке В равен

.

Данный интеграл по поверхности называют интегралом Френеля. Современная теория Максвелла электромагнитных волн для точного решения задачи о распространении световых волн при наличии препятствий приводит к выражению аналогичному интегралу Френеля. Это математическое выражение позволяет вычислять световое возмущение в любой точке наблюдения. Недостатком данного принципа является сложность его практического применения.

4. Если часть волновой поверхности закрыть непрозрачным экраном, то вторичные волны излучаются только открытыми участками поверхности.