Проникновение световых волн в область геометрической тени можно объяснить с помощью принципа Гюйгенса (геометрический принцип). Однако этот принцип не дает сведений об амплитуде, а значит, и об интенсивности волн, распространяющихся в различных направлениях.
Френель дополнил принцип (вложил в принцип Гюйгенса физический смысл) Гюйгенса представлением об интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. Развитый таким образом принцип Гюйгенса получил название принципа Гюйгенса- Френеля.
Френель разработал следующие основные положения, являющиеся дальнейшим развитием теории Гюйгенса.
1) при распределении волн, возбуждаемых источником S0, источник S0 можно заменить системой фиктивных (виртуальных) источников и возбуждаемых ими вторичных волн. В качестве этих источников можно выбрать малые участки любой замкнутой поверхности S, охватывающей S0.
2) Вторичные источники, эквивалентные одному и тому же источнику S0, когерентны между собой, следовательно, в любой точке вне вспомогательной замкнутой поверхности S волны, реально распространяющиеся от источника S0, являющегося результатом интерференции всех вторичных волн.
3) Для поверхности S, совпадающей с волновой поверхностью, мощности вторичного излучения равных по площади участков одинаковы. Каждый вторичный источник излучает свет преимущественно в направлении внешней нормали 
к волновой поверхности в этой точке. Френель исключил возможность возникновения «обратных» вторичных волн, распространяющихся от вторичных источников внутрь области, ограниченной поверхностью S.
4) В том случае, когда часть поверхности S прикрыта непрозрачными экранами, вторичные волны излучаются только открытыми участками поверхности S. Излучение этих участков не зависит от материала, формы и размеров экранов, т.е. осуществляется так, как если бы экранов не было совсем.
Исходя из принципа Гюйгенса – Френеля, можно получить закон прямолинейного распространения света в свободной от препятствий однородной среде.
 |
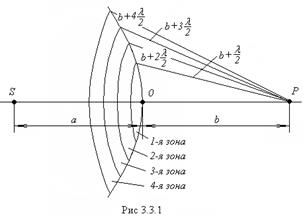Пусть:
S – точечный источник света,
Р – произвольная точка, в которой нужно найти амплитуду колебаний.
Построим:
сферическую волновую поверхность радиуса а,
наименьшее расстояние от поверхности до точки Р равно b,
Амплитуда А зависит от результата интерференции вторичных волн, излучаемых всеми участками dS волновой поверхности.
Для решения этой задачи Френель предложил разбить волновую поверхность на зоны – метод зон Франеля.
- Границей первой зоны служат точки поверхности, находящиеся на расстоянии b + S/2 от точки Р.
- Точки сферы, находящиеся на расстояниях b + 2S/2 от точки Р образуют границы второй зоны Френеля и так далее.
- Расстояние внешнего края т-ной зоны до точки Р равно (рис.3.3.1)
- Колебания, возбуждаемые в точке Р двумя соседними зонами, противоположны по фазе, так как разность хода между ними S/2.
Поэтому при наложении эти колебания ослабляют друг друга:
А= А1 – А2 + А3 – А4 + … . (3.3.1)
А1, А2 – колебания, возбуждаемые каждой зоной порознь.
Величина Ai зависит
- от площади Si i – той зоны
- и угла 
между внешней нормалью к поверхности зоны в какой – либо ее точке и прямой, направленной из этой точки в точку Р.
Можно показать, что площади всех зон Франеля одинаковы:
S
Радиус внешней границы т-ной зоны равен
- радиусы зон возрастают пропорционально 
.
В случае плоской волны 
и 
.
С увеличением номера зоны возрастает угол , и следовательно уменьшается интенсивность излучения зоны в направлении точки Р, т.е. уменьшается амплитуда 
, т.е. А1> А2>…> Аi>…
Можно считать, что в пределах малых изменений i зависимость Ai от i является линейной,
,
тогда
(3.3.2)
Подставив (3.3.2) в (3.3.1), имеем
- результирующее действие в точке Р полностью открытого фронта световых волн, возбуждаемых источником S, равно половине действия одной только центральной зоны Френеля, радиус которой мал, следовательно, с достаточно большой точностью можно считать, что в свободном пространстве свет от источника S в точку Р распространяется прямолинейно.
Поможем написать любую работу на аналогичную тему