Дифракция Фраунгофера на прямоугольной щели.  

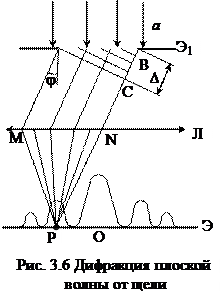
Дифракцию в параллельных лучах или дифракцию плоских волн впервые исследовал немецкий физик И. Фраунгофер в 1821-1822гг. Пусть плоская монохроматическая волна падает нормально на непрозрачный экран Э1 с длинной узкой щелью АВ шириной а (рис. 3.6). Согласно принципу Гюйгенса – Френеля все точки щели можно рассматривать как вторичные источники световых волн, колеблющихся в одной фазе (так как плоскость щели есть часть волновой поверхности падающей плоской волны), и распространяющихся во всех направлениях. Из всего многообразия направлений выберем одно произвольное и будем рассматривать лучи, идущие под углом φ к падающим лучам. Параллельно экрану Э1 поместим линзу Л, а в ее фокальной плоскости – экран Э2, на котором лучи соберутся в некоторой точке Р. Опустим перпендикуляр АС из точки А на крайний луч. АС представляет собой волновую поверхность для лучей, идущих под углом φ и, согласно определению, все точки данной поверхности колеблются в одной фазе. Поэтому отрезок ВС является оптической разностью хода между крайними лучами пучка, ВС = Δ = аsinφ. Поделим участок ВС на отрезки, равные λ/2 и из точек деления проведем плоскости, параллельные АС до пересечения с АВ (эти плоскости перпендикулярны рисунку и поэтому на нем изображены как прямые линии). Эти плоскости поделят щель АВ на равные полоски, которые являются зонами Френеля, т.к. световые волны, идущие от соседних полосок, имеют разность хода λ/2 (см. рис. 3.6). Если число зон будет четным, они попарно погасят друг друга, и в точке Р будет наблюдаться минимум освещенности. Четное число отрезков на участке ВС соответствует условию аsinφ = ±2m λ/2, где m = 1,2,3…Это условие называется условием дифракционного минимума. Из него находятся углы, под которыми наблюдаются дифракционные минимумы на экране. Знак “минус” соответствует лучам, идущим от щели под углом –φ.

Если число зон Френеля нечетно, на экране в точке Р получается дифракционный максимум. Условие дифракционного максимума имеет вид

аsinφ = ±(2m + 1)λ/2, где m = 1, 2, 3…

Это условие определяет углы, соответствующие максимумам освещенности на экране Э2. Число m называется порядком дифракционного максимума или минимума.

В центральной точке экрана О соберутся лучи, идущие в направлении φ = 0, следовательно, без разности хода. В этом направлении щель действует как одна зона Френеля, создавая в точке О самый интенсивный максимум нулевого порядка. Это будет светлая полоса, повторяющая форму щели. Дифракционная картина от щели симметрична относительно точки О и интенсивности максимумов более высоких порядков уменьшаются в пропорции 1 : 0,047 : 0,017 : 0,008…

Дифракционная картина на экране зависит от отношения длины волны падающего монохроматического излучения λ к ширине щели а. Из условия дифракционного минимума , следовательно расстояния от центра картины до минимумов возрастают с уменьшением а. Центральная светлая полоса при этом расширяется. При а«λ вся поверхность щели будет небольшой частью лишь одной зоны Френеля. Такую щель можно считать линейным источником света, колебания от которого будут распространяться в одной фазе и дифракционной картины не наблюдается. При а»λ в центре экрана получается широкая равномерно освещенная полоса, обусловленная беспрепятственным прямолинейным распространением света от источника, и на ее краях наблюдаются очень узкие дифракционные полосы.

При освещении щели белым светом дифракционные максимумы, соответствующие различным длинам волн пространственно разделятся. Чем меньше длина волны, тем ближе к центру экрана будет располагаться ее максимум. Это следует из условия максимума при дифракции от одной щели. В центре экрана объединятся лучи всех длин волн, так как здесь угол φ = 0 и разность хода Δ = 0, поэтому центральный максимум будет белым. Максимумы первого, второго и высших порядков разложатся в спектры, обращенные фиолетовым краем к центру экрана. Подобные спектры расплывчаты, поэтому четкое разделение по длинам волн при дифракции от одной щели получить не удается. Для получения более качественной дифракционной картины свет от источника необходимо пропустить через несколько параллельных щелей.