Дифракция в параллельных лучах (дифракция Фраунгофера). Дифракция на щели

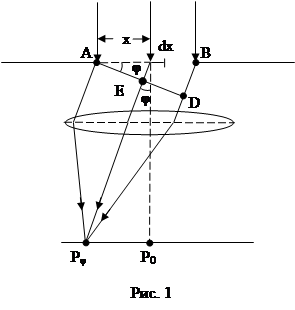
Дифракцию в параллельных лучах называют дифракцией Фраунгофера. Сначала остановимся на дифракции на одной щели. Пусть пучок параллельных лучей падает на экран со щелью шириной а (рис. 1). Каждая точка щели будет являться новым источником колебаний распространяющихся во все стороны. Если за щелью установить собирающую линзу, то лучи идущие под некоторым углом j к первоначальному направлению соберутся в фокальной плоскости линзы. Проведем аналитическое решение. Для чего запишем выражение волны выбранного элемента щели dx, расположенного на расстоянии x от начала щели и просуммируем действие всех элементов. Выражение плоской волны, падающей на щель, запишем в виде

E=E0cosωt           (1)                   

Элемент dx определяет возмущение

,                   (2)                                                  

где  – амплитудное значение.

         Для нахождения результирующего возмущения в любой точке экрана, определяемой углом дифракции j, необходимо знать распределение фаз всех колебаний, проходящих в эту точку. Для этого проведем плоскость АД перпендикулярно направлению дифрагированных лучей. Так как линза не вносит добавочной разности хода, то распределение фазы в т. Р  будет таким же как в плоскости АД. Разность хода лучей идущих от начала щели и от элемента dx будет СЕ= xsinj.

         Элемент dx создает в т. Рj колебание

                                       (3)

а результирующее возмущение в т. Рj будет 

                                (4)

После интегрирования получим

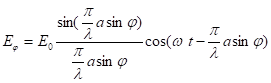                                        (5)

Амплитудное значение запишется в виде

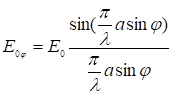                                                  (6)

         Во многих практических случаях (при наблюдении в трубу) угол j мал и можно положить sinφ≈φ, тогда

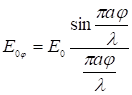                                                 (7)

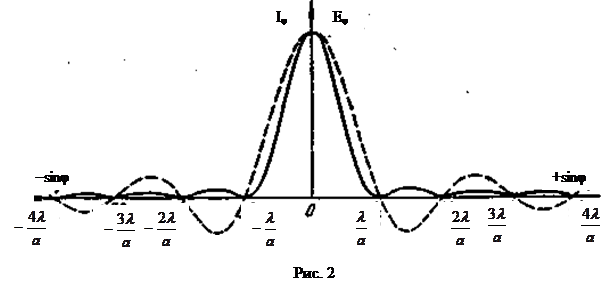
График распределения амплитуды на экране представлен на рис. 2. Е0j обращается в ноль для углов удовлетворяющих условию

,                                      (8)

т.е. для  (9). При промежуточных значениях угла j амплитуда достигает максимальных значений. Наибольший максимум имеет место когда : т.е. φ=0 (10), при этом E0φ=E0. Следующие максимумы найденные графическим сложением определяются условиями

; ; ;             (11)

Интенсивность света 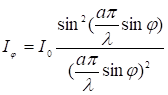                                                      (12)

На графике пунктирная кривая. Расчеты показывают, что интенсивность главного и следующих максимумов относятся как 1:0,47:0,008:0,005 и т.д. Основная часть световой энергии сосредоточена в центральном максимуме.

         Из формулы максимумов и минимумов видно, что на их положение влияет как длина волны, так и ширина щели. С увеличением длины волны l увеличивает угол положение дифракционных максимумов и минимумов. Если падающий свет белый, то в центре дифракционной картины наблюдается белая полоса, переходящая в цветную.

         С увеличением ширины щели а, происходит сближение максимумов и минимумов относительно центра, а при уменьшении ширины щели центральный максимум расплывается и при а=l, т.е. sinj=1, j=p/2 центральный максимум расплывается в бесконечность.