Преломление лучей сферической поверхностью

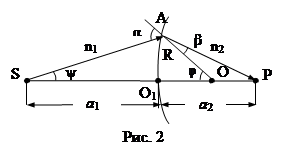
         Пусть имеем сферическую поверхность радиусом кривизны R (рис. 2). S – источник, Р – изображение, ОО¢ – ось системы. Углы a и b – падения и преломления. О – центр кривизны, О¢ – вершина. Если пучок гомоцентрический (имеющий общий центр) сохраняет гомоцентричность после преломления, то каждая точка источника дает одну точку изображения. Такие изображения называются стигматическими. В силу обратимости лучей изображение можно рассматривать как источник и наоборот. В этом случае при стигматичности изображения центры пучков называются сопряженными точками оптической системы. Световые лучи и пучки также называются сопряженными.

         Будем рассматривать пучок настолько узким, т.е. угол y настолько мал, что SA=SO¢, PA=PO¢. Такие пучки называются параксиальными. Все выводы будут справедливы только для параксиальных лучей. Из DАSО 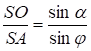; из DАОР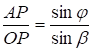  

отсюда 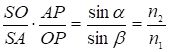                                                                           (7)

или 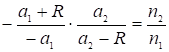 (где n1 и n2 – показатели преломления сред).

Или 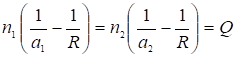 – нулевой инвариант Аббе.

Наиболее удобная формула вида 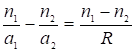                                        (8)

Это соотношение позволяет найти а2, если известно а1. При R>0 поверхность выпуклая, при R<0 – вогнутая. При а2>0 изображение действительное, при а2< – мнимое.

при а1= -¥, 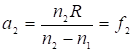 – заднее фокусное расстояние (9) 

при а1= ¥, 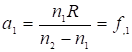  – переднее фокусное расстояние.

При n2=-n1 из (8) имеем

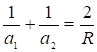 – формула зеркала                       (10)

Для плоского зеркала (R= ¥,)       

а1= -а2                                                      (11)

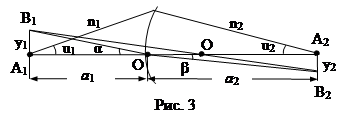Рассмотрим протяженный предмет (рис. 3) А1В1 размером У1, находящийся на расстоянии а1 от вершины сферической поверхности О¢ и центром кривизны О. Найдем выражение для увеличения 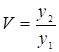. Из DА1В1О¢ 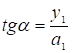, а из DА2О¢В2 имеем .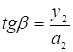

Отношение 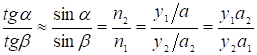                                                            (12)

Отсюда увеличение 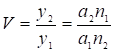              ,                                                  (13) 

знак увеличения зависит от знаков а1 и а2. Для зеркала 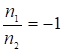, тогда

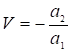                                                   (14)

Угловое увеличение 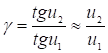                                                                    (15)

Из рис. 3 имеем 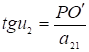, а 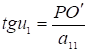, следовательно 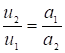, т.е. 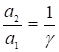. Поэтому  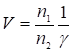                                                                                               (16)

Угловое увеличение g определяется линейным V. Подставляя значение 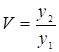  из (12) имеем  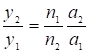и учитывая, что 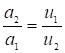, получим  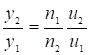, откуда                                         y1n1u1= y2n2u2                                                                  (17)

– теорема Лагранжа-Гельмгольца, а

y1n1sinu1= y2n2sinu2                                                                       (18)

– условие синусов Аббе.