Вещества, у которых свойства зависят от направления, называются анизотропными. Электрические свойства кристаллов для различных направлений электрического вектора ![]() оказываются различными. Анизотропия диэлектрических свойств среды означает, что зависимость поляризованности среды от напряженности электрического поля не может характеризоваться только одной скалярной величиной – диэлектрической восприимчивостью. В анизотропной среде
оказываются различными. Анизотропия диэлектрических свойств среды означает, что зависимость поляризованности среды от напряженности электрического поля не может характеризоваться только одной скалярной величиной – диэлектрической восприимчивостью. В анизотропной среде
Px=ε0æxxEx+ ε0æxyEy+ ε0æxzEz
Py=ε0æyxEx+ ε0æyyEy+ ε0æyzEz (4)
Pz=ε0æzxEx+ ε0æzyEy+ ε0æzzEz
Совокупность æij называется тензором диэлектрической восприимчивости. Можно записать
![]() и
и ![]() , (5)
, (5)
где dij – символ Кроникера. Можно представить ![]() , где
, где![]() – тензор диэлектрической проницаемости. Для прозрачных кристаллов диэлектрический тензор симметричен, т.е. eij=eji. Благодаря тензорной связи
– тензор диэлектрической проницаемости. Для прозрачных кристаллов диэлектрический тензор симметричен, т.е. eij=eji. Благодаря тензорной связи ![]() и
и ![]() и неравенства eх¹eу¹ez направление этих векторов в кристаллах не совпадают.
и неравенства eх¹eу¹ez направление этих векторов в кристаллах не совпадают.
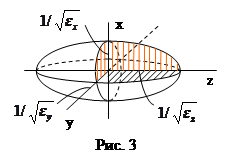
В квадратичной форме тензор eij в кристалле относительно главных осей представляется эллипсоидом
 eхх2+eуу2+ezz2=1 (6)
eхх2+eуу2+ezz2=1 (6)
Главными осями этого эллипсоида являются ![]() (рис. 3). Относительно главных осей этого эллипсоида тензор диэлектрической проницаемости является диагональным
(рис. 3). Относительно главных осей этого эллипсоида тензор диэлектрической проницаемости является диагональным
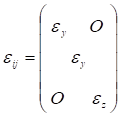 (7)
(7)
Оси х, у, z называют главными осями тензора диэлектрических проницаемостей.
При распространении плоской электромагнитной волны ![]() волновой вектор
волновой вектор ![]() перпендикулярен поверхности одинаковой фазы, т.е. показывает направление распространения волнового фронта. Фазовая скорость
перпендикулярен поверхности одинаковой фазы, т.е. показывает направление распространения волнового фронта. Фазовая скорость ![]() волны направлена по этому вектору, это направление принимается за направление распространения волны и характеризуется единичным вектором
волны направлена по этому вектору, это направление принимается за направление распространения волны и характеризуется единичным вектором ![]() . Волна распространяется перпендикулярно
. Волна распространяется перпендикулярно ![]() и
и ![]() . Поток же энергии (вектор Пойтинга) направлен перпендикулярно
. Поток же энергии (вектор Пойтинга) направлен перпендикулярно ![]() и
и ![]() . Направление потока называется лучом. Энергия электромагнитной волны движется с групповой скоростью
. Направление потока называется лучом. Энергия электромагнитной волны движется с групповой скоростью ![]() . Она не совпадает с направлением
. Она не совпадает с направлением ![]() . За единичный вектор в направлении луча принимается вектор
. За единичный вектор в направлении луча принимается вектор ![]() . Так как векторы
. Так как векторы ![]() и
и ![]() в анизотропной среде не колинеарны, направление распространения волны и луча не совпадает.
в анизотропной среде не колинеарны, направление распространения волны и луча не совпадает.
Векторы ![]() и
и ![]() перпендикулярны
перпендикулярны ![]() ;
; ![]() и
и ![]() , так же перпендикулярны
, так же перпендикулярны ![]() ,
, ![]() и
и ![]() перпендикулярны соответственно
перпендикулярны соответственно ![]() и
и ![]() . Это означает, что
. Это означает, что ![]() ,
, ![]() ,
, ![]() ,
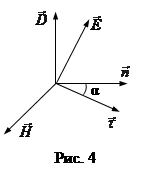
, ![]() лежат в одной и той же плоскости перпендикулярной
лежат в одной и той же плоскости перпендикулярной ![]() (рис. 4). Угол между
(рис. 4). Угол между ![]() и
и ![]() равен углу между
равен углу между ![]() и
и ![]() . В связи с этим можно записать связь между u и u; u=ucosa (8)
. В связи с этим можно записать связь между u и u; u=ucosa (8)
 Учитывая выражение плоской волны, и пользуясь уравнениями Максвелла с учетом, что
Учитывая выражение плоской волны, и пользуясь уравнениями Максвелла с учетом, что 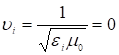 выводится уравнение Френеля
выводится уравнение Френеля
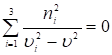 (9)
(9)
 Это уравнение позволяет найти фазовую скорость в направлении, характеризуемом направляющими косинусами n1, n2, n3. Для нахождения корней уравнения строится график функции
Это уравнение позволяет найти фазовую скорость в направлении, характеризуемом направляющими косинусами n1, n2, n3. Для нахождения корней уравнения строится график функции 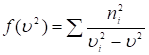 (рис. 5). Вертикальные пунктирные линии проведены через точки ui2. Из этой зависимости имеем два действительных значения ui2, удовлетворяющих уравнению. Это означает, что в заданном направлении могут распространяться волны с двумя различными фазовыми скоростями u¢ и u¢¢, заключенными между наименьшей и средней, средней и наибольшей из скоростей. Векторы
(рис. 5). Вертикальные пунктирные линии проведены через точки ui2. Из этой зависимости имеем два действительных значения ui2, удовлетворяющих уравнению. Это означает, что в заданном направлении могут распространяться волны с двумя различными фазовыми скоростями u¢ и u¢¢, заключенными между наименьшей и средней, средней и наибольшей из скоростей. Векторы ![]() и
и ![]() этих волн взаимно перпендикулярны. Аналогичное уравнение Френеля получается и для лучевых скоростей
этих волн взаимно перпендикулярны. Аналогичное уравнение Френеля получается и для лучевых скоростей
![]() (10)
(10)
Здесь также две волны, распространяющиеся в данном направлении с двумя различными групповыми скоростями имеют перпендикулярные направления поляризации, т.е. векторы ![]() и
и ![]() взаимно перпендикулярны.
взаимно перпендикулярны.
Если в уравнении тензора eij (6) произвести замену ![]() , то получим так же эллипсоид, который является эллипсоидом лучевых скоростей
, то получим так же эллипсоид, который является эллипсоидом лучевых скоростей
x2/υx2+ y2/υy2+ z2/υz2=1 (11)
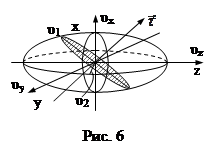 υх, υу, υz – главные лучевые скорости (рис. 6). Выберем направления распространения луча
υх, υу, υz – главные лучевые скорости (рис. 6). Выберем направления распространения луча ![]() и через центр эллипсоида проведем плоскость перпендикулярно вектору
и через центр эллипсоида проведем плоскость перпендикулярно вектору ![]() . В сечении эллипсоида этой плоскостью образуется эллипс, главные полуоси которого υ1 и υ2. Вектор
. В сечении эллипсоида этой плоскостью образуется эллипс, главные полуоси которого υ1 и υ2. Вектор ![]() световой волны, распространяющейся по лучу, может колебаться только параллельно главным осям этого эллипса. Соответствующие групповые скорости равны длинам его главных полуосей υ1
и υ2. Таким образом, в произвольном направлении
световой волны, распространяющейся по лучу, может колебаться только параллельно главным осям этого эллипса. Соответствующие групповые скорости равны длинам его главных полуосей υ1
и υ2. Таким образом, в произвольном направлении ![]() возможно распространение лишь двух линейно поляризованных волн с различными лучевыми (групповыми) скоростями. Если сечение эллипсоида вырождается в окружность, то υ1=υ2
и поэтому любой радиус окружности является главной полуосью. В этом случае вектор
возможно распространение лишь двух линейно поляризованных волн с различными лучевыми (групповыми) скоростями. Если сечение эллипсоида вырождается в окружность, то υ1=υ2
и поэтому любой радиус окружности является главной полуосью. В этом случае вектор ![]() может колебаться в любом направлении перпендикулярном
может колебаться в любом направлении перпендикулярном ![]() .
.
В направлении перпендикулярно плоскости кругового сечения эллипсоида лучевых скоростей, всем лучам соответствует одна и та же лучевая скорость, а векторы ![]() могут колебаться в любом направлении плоскости кругового сечения, т.е. в этом направлении анизотропия среды не проявляется. Направление, перпендикулярное круговому сечению, называется оптической осью анизотропной среды.
могут колебаться в любом направлении плоскости кругового сечения, т.е. в этом направлении анизотропия среды не проявляется. Направление, перпендикулярное круговому сечению, называется оптической осью анизотропной среды.
Эллипсоид с тремя различными по значению главными осями имеет два круговых сечения. Таким образом, если у эллипсоида все главные оси различны, то соответствующая среда имеет две оптические оси. Такие кристаллы называются двуосными.
Если у эллипсоида две оси равны между собой, то он является эллипсоидом вращения вокруг третьей оси. В этом случае имеется только одна оптическая ось, и кристалл является одноосным. Если у эллипсоида все оси равны, то он превращается в сферу. В этом случае все направления эквивалентны и кристалл будет оптически изотропным.
Вместо лучей можно рассматривать распространение волн, движение которых характеризуется вектором ![]() , нормальным к поверхности волнового фронта. В этом случае получается эллипсоид волновых нормалей.
, нормальным к поверхности волнового фронта. В этом случае получается эллипсоид волновых нормалей.
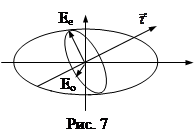 Через луч, направленный под углом к оптической оси, и оптическую ось можно провести плоскость, которая называется главной (рис. 7). У луча, вектор
Через луч, направленный под углом к оптической оси, и оптическую ось можно провести плоскость, которая называется главной (рис. 7). У луча, вектор ![]() которого направлен перпендикулярно главной плоскости скорость не зависит от направления и равна лучевой скорости, которая направлена коллинеарно оптической оси. Этот луч называется обыкновенным. Его скорость υ0 и показатель преломления n0=c/υ0. У луча, вектор
которого направлен перпендикулярно главной плоскости скорость не зависит от направления и равна лучевой скорости, которая направлена коллинеарно оптической оси. Этот луч называется обыкновенным. Его скорость υ0 и показатель преломления n0=c/υ0. У луча, вектор ![]() которого лежит в главной плоскости, скорость зависит от направления. Этот луч называется необыкновенным, его скорость uе и показатель преломления nе=c/υе. Кристаллы с υ0<υе
– отрицательные, а с υ0>υе – положительные.
которого лежит в главной плоскости, скорость зависит от направления. Этот луч называется необыкновенным, его скорость uе и показатель преломления nе=c/υе. Кристаллы с υ0<υе
– отрицательные, а с υ0>υе – положительные.
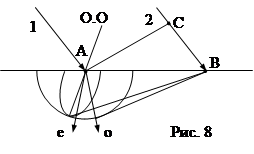 В связи с тем, что внутри кристалла возможно распространение лишь двух лучей с различными лучевыми скоростями, преломление луча на поверхности кристалла приводит к возникновению двойного лучепреломления. Двойное лучепреломление анализируется с помощью построения Гюйгенса (рис. 8). При падении параллельного пучка лучей на поверхность кристалла под каким–либо углом к оптической оси происходит разделение луча, которое объясняетсятся следующим образом. Точка А (падение луча 1) принимается за центр сечения лучевой поверхности. За время прохождения луча 2 расстояния СВ до поверхности, луч 1 распространяется в кристалле. При этом для обыкновенного луча лучевая поверхность представляет собой полусферу, а для необыкновенного луча – эллиптическое сечение, большая полуось которого направлена вдоль оптической оси О.О. Из точки В проводятся касательные к окружности и эллипсу. Прямые, проведенные через точку А и точки касания, являются направлениями распространения обыкновенного и необыкновенного лучей о и е. Эти лучи линейно поляризованы во взаимно перпендикулярных плоскостях.
В связи с тем, что внутри кристалла возможно распространение лишь двух лучей с различными лучевыми скоростями, преломление луча на поверхности кристалла приводит к возникновению двойного лучепреломления. Двойное лучепреломление анализируется с помощью построения Гюйгенса (рис. 8). При падении параллельного пучка лучей на поверхность кристалла под каким–либо углом к оптической оси происходит разделение луча, которое объясняетсятся следующим образом. Точка А (падение луча 1) принимается за центр сечения лучевой поверхности. За время прохождения луча 2 расстояния СВ до поверхности, луч 1 распространяется в кристалле. При этом для обыкновенного луча лучевая поверхность представляет собой полусферу, а для необыкновенного луча – эллиптическое сечение, большая полуось которого направлена вдоль оптической оси О.О. Из точки В проводятся касательные к окружности и эллипсу. Прямые, проведенные через точку А и точки касания, являются направлениями распространения обыкновенного и необыкновенного лучей о и е. Эти лучи линейно поляризованы во взаимно перпендикулярных плоскостях.
Поможем написать любую работу на аналогичную тему

