Исследования показали, что показатель преломления среды зависит от частоты или длины волны, т.е. n=f(ω). Эта зависимость и называется дисперсией света. Очень наглядный метод исследования дисперсии материала был применен Ньютоном. Это метод скрещенных призм. Пучок света проходит через две призмы установленные таким образом, чтобы преломляющие ребра их были расположены перпендикулярно друг другу. Цветная полоса, получающаяся после прохождения света одной призмы, отклоняется второй призмой. На экране получается окончательная форма, определяемая величиной дисперсии обеих призм. Зависимость между показателем преломления и частотой света может быть весьма сложной. Если показатель преломления увеличивается с увеличением частоты ω, то дисперсия называется нормальной, если зависимость имеет обратный характер, то дисперсия называется аномальной. Аномальную дисперсию наблюдать очень трудно, так как она обычно располагается в области поглощения света веществом.
Рождественский, используя интерферометр и спектрограф, предложил метод крюков, позволивший значительно повысить точность измерения дисперсии в непосредственной близости к полосе поглощения.
Объяснение явления дисперсии света удалось объяснить только после более глубокого рассмотрения взаимодействия световых волн с веществом.
Для вывода зависимости показателя преломления от частоты нужно найти как зависит диэлектрическая проницаемость от частоты (длины) переменного электрического поля. Дело в том, что показатель преломления связан с фазовой скоростью 
, а скорость определяется из электромагнитной теории Максвелла 
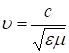. Откуда 
. Для большинства прозрачных тел μ=1 и следовательно 
.
Будем рассматривать молекулы или атомы диэлектрика как систему, в которую входят электроны, находящиеся в молекулах (атомах) в положении равновесия. Под влиянием внешнего поля эти заряды смещаются из положения равновесия на расстояние r, превращая атом в электрический диполь с моментом 
. Если в единице объема среды находится N атомов, то электрический момент единицы объема (поляризация) среды будет 
. Зная поляризацию среды можно вычислить ее диэлектрическую проницаемость ε, так как индукция 
. Следовательно
(1)
Таким образом, задача сводится к определению смещения электрона r под действием внешнего периодически меняющегося поля при учете сил действующих на электрон, входящий в состав атома, со стороны частей этого атома и окружающих атомов.
В связи с этим, запишем уравнение движения электрона. Световую волну запишем в виде 
, следовательно, сила со стороны этого поля на электрон будет меняться таким же образом. На смещенный электрон со стороны атома будет действовать упругая сила, пропорциональная смещению, т.е. – 
. Кроме того, необходимо учесть и силу, приводящую к затуханию возникающих колебаний электрона (сила сопротивления), которая будет пропорциональна скорости электрона, т.е. – 
.
Таким образом, уравнение движения запишется следующим образом
(2)
Разделим на m и перенесем все слагаемые с 
в левую сторону, получим
,
обозначим 
и 
, тогда уравнение перепишется в виде
(3)
Это уравнение колебания, собственная частота которого 
.
Собственные колебания такой связанной системы в твердом теле быстро затухают и остаются только вынужденные, которые происходят по закону вынуждающей силы. Поэтому решением этого уравнения будет 
. Подставляя значения смещения в уравнение (3), получим
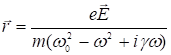. (4)
Подставляя его в выражение для n (1) получим
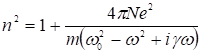. (5)
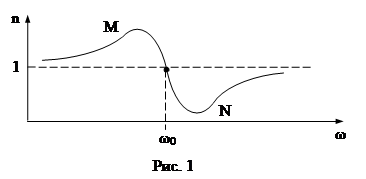Таким образом, показатель преломления зависит от частоты ω внешнего поля. В области ω=0 до ω=ω0 n>1 и возрастает при возрастании ω (нормальная дисперсия). От ω=ω0
до ω= ∞ n<1 и также возрастает от -∞ до 1 (нормальная дисперсия).
График зависимости n(ω) представлен на рис. 1. В области ω0 (MN) показатель преломления с увеличением частоты уменьшается. Это область аномальной дисперсии. Она связана с поглощением света.
Если учесть, что в веществе может быть несколько сортов заряженных частиц с массами mi и собственными частотами ω0i и зарядами еi, то уравнение дисперсии запишется следующим образом
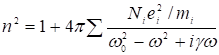(6)
Рассмотрим связь дисперсии и поглощения, т.е. показателя преломления n и коэффициента поглощения a.
Эмпирический закон поглощения Бугера имеет вид I=I0e-αl, где a – коэффициент поглощения. Комплексный показатель преломления связан с коэффициентом экстиниции æ, 
, волновой вектор 
. Падающая световая волна 
, а выходящая из вещества толщиной х будет
, (7)
где амплитудное значение 
(8). Для интенсивности, следовательно,
(9)
Сравнивая с эмпирическим законом, запишем выражение для коэффициента поглощения
(10)
Поможем написать любую работу на аналогичную тему