Дрейф в неоднородном магнитном поле

Строгое рассмотрение движения заряженных частиц в неоднородном магнитном поле требует громоздких математических выкладок.

Изменение величины индукции магнитного поля (градиент) приводит к изменению циклотронного радиуса частицы , что и является причиной градиентного дрейфа. Ввиду того, что циклотронное вращение происходит в плоскости, перпендикулярной к силовым линиям, дрейф вызывается только градиентом магнитного поля поперёк его направления, который обозначается как .  Если через  обозначить смещение среднего положения частицы за один оборот, то дрейфовая скорость определяется соотношением:

                                       .

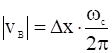Циклотронный радиус меняется непрерывно, тогда можно доказать, что , где  – изменение циклотронного радиуса на его собственной длине (). Таким образом:

                         .

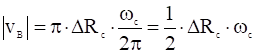Так как:

                        ,
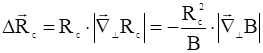то:

                               .
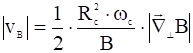Подставляя 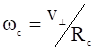, получим:

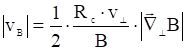                                .                                       (2)

Формула (2) определяет скорость градиентного дрейфа только по величине, но не по направлению. Чтобы определить направление дрейфовой скорости, нужно записать (2) в векторной форме. Составляющую градиента в направлении, перпендикулярном к , можно представить как векторное произведение , где  – единичный вектор в направлении магнитного поля. Тогда формулу (2) можно записать в виде:

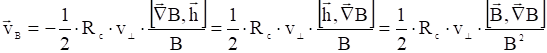. (3)

Градиентный дрейф приводит к разделению зарядов.

Изменение направления магнитных полей может быть описано как искривление магнитных силовых линий. Центр циклотронной окружности движется по искривлённой силовой линии и можно считать, что на него действует центробежная сила, величина которой:

                                        ,
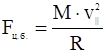где  – радиус кривизны силовой линии.

Эта сила направлена вдоль радиуса кривизны, то есть по нормали к силовой линии. Если рассматривать радиус кривизны, как вектор , направленный от центра кривизны с силовой линии, то в векторном виде центробежная сила:

                                     ,

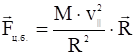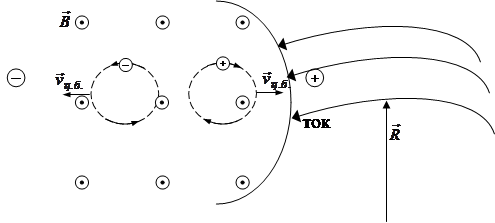
тогда скорость центробежного дрейфа:                                                            
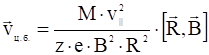                                         .                                     (4)

Скорости градиентного и центробежного дрейфов зависят от заряда частицы, так что противоположно заряженные частицы дрейфуют в противоположных направлениях. Следовательно, неоднородность магнитного поля возбуждает в плазме дрейфовые токи, приводящие к разделению зарядов. Плотность дрейфового тока:

                                       ,
откуда для градиентного дрейфа:

                                ,
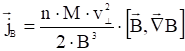так как 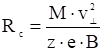, и для центробежного дрейфа:

                                ,
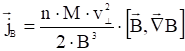где  – концентрация частиц.