Методика изучения межличностных отношений и комплектования малых групп

Задача первичного комплектования малых групп может быть решена с использованием методики В. Шультца (ОМО) на основе изучения характерных особенностей индивидуальной ориентации человека по отношению к другим людям. В основе процедуры лежат установленные закономерности сочетания характерных способов поведения двух индивидов в межличностном взаимодействии, предопределенных их социальным опытом.

Характерные способы поведения двух индивидов в межличностном взаимодействии могут быть либо совместимыми, либо нет. Создатель Опросника межличностных отношений В. Шультц определяет межличностную совместимость как такие отношения между двумя или более индивидами, при которых достигается та или иная степень взаимного удовлетворения межличностных потребностей. Прогнозирование совместимости осуществляется посредством вычисления для каждой конкретной пары (диады) значения дискриминантной функции.

Процедура комплектования малых групп с использованием Опросника межличностных отношений (ОМО) включает:

• обследование всех потенциальных членов группы по методике ОМО;

• обработку результатов обследования и получение «сырых» баллов
по показателям: le, Iw, Ce, Cw, Ae, Aw;

• вычисление для всех предполагаемых составов групп коэффициентов,
характеризующих совместимость межличностной ориентации диады:

Коэффициента взаимной совместимости: rK - |eA-wB;+|eB-wA;.

Коэффициента инициации: оК = (eA-wA)+(eB-wB).

Коэффициента взаимного обмена: хК - |(eA+wA)-(eB+wB);.

где:

еА — выраженное поведение лица А;

еВ — выраженное поведение лица В;

wA — требуемое поведение лица А;

wB — требуемое поведение лица В.

Отдельные типы коэффициентов совместимости можно подсчитать для каждой из областей межличностных потребностей. Тогда из комбинации создают индексы совместимости, которые могут быть использованы при решении различных проблем:

•  подстановку рассчитанных значений показателей в уравнение дис-
криминантной функции и вычисление ее величины:

Y(ij) - 0,08 r rКС + 0,25 г оКС + 0,07 г гК - 2,83,

где:

ij — номера членов группы;

0,08; 0.25; 0,07  — коэффициенты дискриминантной функции;

2,83 — константа.

•  сравнение полученной величины с критической (Укр = 0 );

при Y < 0 пара относится к категории совместимой, при Y > 0 — к несовместимой.

•  комплектование групп.

Пример комплектования групп:

Необходимо скомплектовать 4 микрогруппы из 8 человек (4 старших и 4 подчиненных).

Результаты диагностики совместимости в виде значений дискриминантных функций представлены в таблице.

Результаты диагностики совместимости с использованием ОМО

Находим минимальное значение в таблице: — 4.32 — для группы в составе: старший (1) — подчиненный (8). Следующее минимальное значение: — 2.96 — для группы, образованного из старшего (4) и подчиненного (7). Повторяя процедуру для других, получаем: группа, состоящая из старшего (3) и подчиненного (6), и группа, включающая старшего (2) и подчиненного (5).

Таким образом, сформировано 4 группы в составе:

1) 1-й — 8-й;

2) 4-й - 7-й;

3) 3-й — 6-й:

4) 2-й — 5-й.

При переукомплектовании малых групп в качестве основного диагностического средства может быть использована социометрия. При комплектовании коллективов она используется для изучения межличностных оценок, симпатий и антипатий членов группы, возникших в результате совместной деятельности и общения, а также для определения оптимальных составов малых групп.

Таблица 4

Пример заполнения матрицы 1

Процедура комплектования в данном случае включает:

•        проведение социально-психологического обследования с использованием социометрических критериев-вопросов анкеты (Приложение 3);

•        составление прямоугольных матриц по результатам опроса;

•        преобразование прямоугольных матриц в треугольные;

•        назначение старших групп и составление для них матриц;

•        комплектование групп, состоящих из двух, трех и т. д. человек.

Пример 1. Комплектование групп, состоящих из двух человек

Имеется заполненная прямоугольная матрица (1) (см. табл. 5). Преобразуем прямоугольную матрицу (1) в треугольную (2), значения элементов которой вычисляем по формуле (см. табл. 5):

Таблица 5

Пример заполнения треугольной матрицы (2)

Пусть старшие групп представлены под номерами: 1, 3, 4, 13. Составляем для них матрицу (3), элементы которой берутся из треугольной матрицы (2).

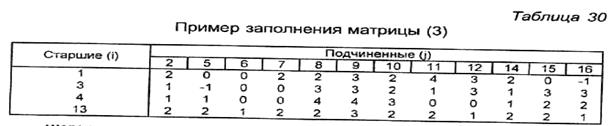
Формирование групп

Для каждой строки матрицы (3), т. е. для каждого старшего группы выбираем только один элемент, так чтобы:

• сумма выбранных элементов была максимальной;

• из одного столбца был выбран только один элемент, так как один
человек не может быть в двух группах.

Для этого определяем максимальные элементы в каждой строке:

•  в первой строке — 11-й так как С(1.11) = 4.

•  во второй строке — 8-й, 9-й, 12-й, 15-й, и 16-й, так как С(3.8) —
С(3.9) = С(3.12) = С(3.15) = С(3.16) = 3.

•  в третьей строке — 8-й и 9-й, так как С(4.8) = С(4.9) = 4.

•  в четвертой строке — 9-й, так как С(13.9) = 3.

Определяем состав групп: в данном случае это пары сотрудников 1-й — 11-й; 3-й — 16-й; 4-й— 8-й; 13-й — 9-й.

Выбор пар 1-й — 11-й и 13-й —9-й очевиден, так как в первой строке содержится только один максимальный элемент С(1.11) = 4 и в четвертой — тоже один — С(13.9) = 3.

Тогда в третьей строке после вычеркивания 9-го столбца (один человек не может быть в двух группах) остается только один максимальный элемент С(4.8) = 4.

Подбор подчиненного к старшему под № 3 (вторая строка) проводится по правилу суммы оставшихся элементов выбранного столбца. Это правило говорит о том, что взаимная психологическая связь подчиненного под № 16 со старшим под № 3, с которым он образует группу, максимальна, а со старшими под № 1, 4, 13 — минимальна.

Для данного случая по матрице (3) определяем суммы элементов 12-го, 15-го и 16-го столбцов, исключая элементы на пересечении этих столбцов со второй строкой (со старшим под № 3):

С(1.12) + С(4.12) + С(13.12) = 3 + 0 + 1 =4

Q1.15) + С(4.15) + С(13.15) = 0 + 2 + 2 = 4

С(1.16) + С(4.16) + С(13.16) = -1+2+1=2

Поскольку сумма оставшихся элементов столбца j = 16 для строки           i = 3 минимальна, так как равна 2, то образуется группа в составе 3-й — 16-й, у которой С(3.16) = 3.

Таким образом, сформированы четыре группы:

1) 1-й — 11-й,

2) 3-й - 16-й,

4) 13-й -9-й,                      

3) 4-й — 8-й.

Пример 2. Комплектование групп, состоящих из трех человек

За основу берем матрицу (3). Из нее исключаем столбцы 8, 9, 11, 16 (т. е. подчиненных, уже вошедших в группы). Вычисляем взаимную психологическую связь выбранных пар (1.11), (3.16), (4.8), (13.9) с оставшимися членами группы под № 2,5,6,7,10,12,14,15 и формируем матрицу (4). При этом используем элементы матрицы (2).

Так взаимная психологическая связь пары (1.11) с членом группы под № 2 будет складываться из суммы значений взаимных оценок пар; 1-й — 11-й, 1-й —2-й, 11-й — 2-й и будет равна числу 7, т. е. 0(1.11) + С(1.2) + С(11.2) = 4 + 2+1=7.

Аналогично производим расчет для всех пар и для всех оставшихся членов коллектива.

В результате матрица (4) будет иметь вид:

Таблица 6

Пример заполнения матрицы (4)

• определяем позиции максимальных и близких к ним элементов в
каждой строке;

• строкам, имеющим единственный максимальный элемент, меньший по сравнению с максимальными элементами других строк, отдается предпочтение, т. е. образуются тройки (3.16.12), (3.11.14);

• две другие тройки образуются с учетом правила минимальной суммы оставшихся элементов выбранного столбца, т. е. образуются тройки
(4.8.10) и (13.9.5).

Таким образом, скомплектованы четыре смены, каждая из которых состоит из трех человек:

1) 1, 11, 14;

2)3,16,12;

3)4,8, 10;

4) 13,9. 15.

На практике при изучении межличностных отношений в коллективах и комплектовании малых групп могут быть получены различные наборы взаимных оценок членов коллектива (как в целом завышенные, так и заниженные). В табл. 7 приведены возможные варианты сочетания взаимных оценок и указана степень благоприятности сочетаний в паре для выполнения совместной деятельности, выраженная в 5 -балльной шкале: 5 — очень высокая, 4 — высокая, 3 — средняя, 2 — низкая, 1 — крайне низкая.

Таблица 7

Сочетания взаимных оценок в паре «старший — подчиненный» по «прямому» критерию — А шкалы приемлемости: выбор и отвержение для совместной деятельности

В практической деятельности психолога важно уметь осуществлять экспресс-диагностику межличностных отношений в малых группах. Важно иметь в виду, что предлагаемые выше методы диагностики межличностных отношений в коллективах и основанные на них алгоритмы комплектования малых групп имеют два видимых недостатка. Первый из них заключается в том, что акцент на достижение благоприятных эмоциональных отношений (психологической совместимости) отодвигает как бы на второй план аспект деятельности изучаемых малых групп. Второй сопряжен с относительно трудоемким процессом обработки результатов социально-психологического обследования (прежде всего социометрического) и, следовательно, невозможностью оперативно отслеживать динамику социально-психологических процессов в коллективе.

Преодолеть эти недостатки призван метод экспресс-диагностики межличностных отношений — психометрический метод Дюке. При этом следует оговориться, что данный метод рассматривается лишь как вспомогательный,

Психометрический метод Дюке может использоваться как метод, дополняющий и уточняющий информацию социометрического обследования в ситуациях экстренного формирования различных коллективов и групп, а также как метод экспресс-диагностики, направленный на оперативное отслеживание динамики межличностных отношений в малых группах. Главное преимущество метода заключается в том, что он относительно прост в проведении обследования и обработке результатов, а следовательно, не требует больших временных и трудовых затрат.

Основным критерием оценки межличностных отношений в предлагаемой методике служит дистанция межличностного общения. Респонденты (опрашиваемые) фиксируют приемлемую дистанцию общения с тем или иным коллегой на специальной схеме, моделирующей некоторое замкнутое пространство. Психолог сводит индивидуальные оценки членов группы (расстояние на схеме в мм) в матрицу взаимных оценок приемлемой дистанции межличностного общения (табл. 8).

Матрицы имеют размерность N x N, где N— общее число членов группы по списку. Составление (заполнение матриц) осуществляется следующим образом. Из регистрационного листа 1 переносят оценки (расстояния в мм) в столбец 1 матрицы. На пересечении строки 1 и столбца 1 ставится знак «х». Таким же образом заполняются и все остальные столбцы матрицы. Поскольку элементом матрицы является оценка, которую i-й член группы дал j-му, следовательно, i-й столбец представляет набор оценок, данных i-м членом группы всем остальным, j-я строка — набор оценок, полученных j-м членом группы от остальных.

Таблица 8

Пример заполнения матрицы (5)

Преобразуем прямоугольную матрицу (5) в треугольную (6), значения элементов которой вычисляем по формуле: С сум.(ij) = С (ij) + С (ij), т. е. складываем диагональные парные оценки, взятые из матрицы (1).

Таблица 9

Пример заполнения матрицы (6)

Уменьшение этой дистанции (показатель суммы взаимных оценок) между членами группы в процессе совместной деятельности может свидетельствовать об улучшении отношений в диаде, достижении психологической совместимости. Напротив, резкое увеличение этого показателя дает повод задуматься о назревающем конфликте в группе и, следовательно, необходимости поиска причин и путей локализации такого конфликта.