Квантовая теория спонтанного и низкоэнергетического вынужденного деления, базирующаяся на стационарном формализме многочастичной теории ядерных реакций и теории открытых ферми-систем , использующая основные достижения традиционной теории деления и квантовомеханических подходов работ и опирающаяся на понятия волновых функций делящегося ядра и фрагментов деления, амплитуд парциальных делительных ширин и делительных фаз, была развита в работах .
В рамках квантовой теории двойного деления деление рассматривается как распад квазистационарного состояния делящегося ядра, описываемого волновой функцией 
, которая удовлетворяет уравнению Шредингера:
(1.7)
где 
– гамильтониан ядра 
в с.ц.м., 
, 
совпадает с точностью до знака с энергией связи ядра, 
– полная ширина распада ядра во все открытые каналы.
С использованием техники проекционных операторов многочастичной теории ядерных реакций и теории открытых Ферми-систем волновая функция делящегося ядра представляется в виде:
(1.8)
где оператор 
проектирует состояния ядра на внутреннюю (оболочечную) область конфигурационного пространства, связанную с полным набором координат 
ядра в с.ц.м.. В этой области ядро имеет односвязную форму и может быть описано при использовании ортонормированного, но ограниченного базиса 
многочастичных оболочечных функций, строящихся в рамках обобщенной модели ядра с учетом нормальных и сверхтекучих нуклон-нуклонных корреляций и коллективных мод движения, где индекс 
принимает дискретный и конечный ряд значений. В этом случае оператор можно представить как
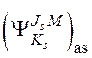(1.9)
Волновая функция 
включает в себя полную информацию об эволюции делящегося ядра от начальной конфигурации в первой яме потенциала деформации через седловые точки потенциала деформации с учетом ПДС в состояния делительных мод 
в окрестности точки разрыва делящегося ядра на фрагменты деления. Для спонтанного деления функция совпадает с волновой функцией 
(1.2), где проекция 
соответствует основному состоянию 
делящегося ядра в первой яме потенциала деформации, поскольку проекция сохраняется в процессе деления. В случае вынужденного околопорогового деления, когда в первой яме потенциала деформации образуется составное ядро с большой энергией возбуждения (
), оболочечная волновая функция делящегося ядра в первой яме потенциала деформации представляет собой суперпозицию волновых функций с фиксированными значениями :
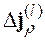(1.10)
где коэффициенты 
учитывают Кориолисово смешивание проекций спина для высоколежащих по энергии и сложных по своей квазичастичной структуре состояний ядра .
Оболочечная волновая функция делящегося ядра трансформируется при переходе этого ядра к точке разрыва к виду :
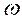(1.11)
где коэффициент 
учитывает динамику перехода делящегося ядра при сохранении квантовых чисел 
из состояния составного ядра 
в первой яме потенциала деформации в состояние делительной моды при учете ПДС на внутренней и внешней седловых точках потенциала деформации.
Оператор 
проектирует состояние делящегося ядра на область конфигурационного пространства (кластерную область), где первичные фрагменты деления уже сформированы. Волновая функция 
(1.8) квазистационарного состояния с 
делящегося ядра в кластерной области представляется формулой
(1.12)
где 
– многочастичная функция Грина в кластерной области, которая удовлетворяет уравнению:
(1.13)
При построении волновой функции делящегося ядра в кластерной области 
для двойного деления используются каналовые функции 
, обладающие правильными трансформационными свойствами при обращении времени:
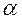(1.14)
где фигурные скобки обозначают векторную связь моментов; шаровая функция 
, соответствующая относительному движению фрагментов деления с орбитальным моментом 
, зависит от телесного угла 
, определяющего направление радиуса-вектора 
в л.с., причем 
и 
– координаты центров тяжести фрагментов с массовыми числами 
и 
(
); волновые функции 
, описывающие состояния аксиально-симметричных фрагментов, имеют вид, аналогичный формуле (1.2) с заменой 
на 
; каналовые индексы 
, отвечающие различным физическим каналам деления, определяются как 
, 
.
Допустим, что взаимодействие фрагментов деления не приводит к перестройке их нуклонного состава, т.е. сохраняет без изменения значения 
, 
. В этом случае гамильтониан можно представить в форме:
(1.15)
где 
– гамильтониан невзаимодействующих фрагментов деления, а 
– кулоновский и ядерный потенциал взаимодействия указанных фрагментов. Функцию Грина (1.13) можно определить как
(1.16)
где индекс 
(
) включает большее (меньшее) из значений модулей радиусов векторов 
и 
, входящих в определение полного набора и 
координат делящегося ядра, 
и 
– регулярные и нерегулярные функции, нормированные на 
-функцию по энергии, которые можно представить в виде:
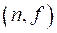. (1.17)
В формуле (1.17) радиальные формфакторы 
и 
являются решениями радиального уравнения Шредингера, описывающего относительное движение фрагментов деления с энергией 
:
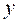(1.18)
где
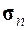, (1.19)
причем 
– скорость относительного движения фрагментов деления; 
– приведенная масса фрагментов. Формфакторы и имеют следующие асимптотики при 
:
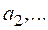(1.20)
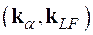, (1.21)
где 
– потенциальные делительные фазы.
Оболочечная волновая функция 
моды деления , описывающей предразрывную конфигурацию делящегося ядра, в кластерной области, где формируются первичные фрагменты деления, переходит в функцию 
, асимптотика которой при больших представляется в виде :
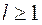(1.22)
где 
– амплитуда парциальной делительной ширины, определяемая в работах как
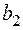(1.23)
Согласно закону сохранения четности в процессе деления величина отлична от нуля при выполнении условия: 
. При учете ортогональности каналовых функций (1.14), соответствующих различным делительным модам и значениями проекций , выражение для полной делительной ширины принимает вид:
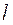(1.24)
Для кластерной области используется адиабатическое приближение, основанное на том, что радиальное относительное движение фрагментов деления происходит быстрее, чем их угловое относительное и вращательное движения.
Для применимости адиабатического приближения должны выполняться следующие условия. Во-первых, кинетическая энергия 
относительного движения первичных фрагментов в окрестности точки разрыва делящегося ядра 
для всех открытых каналов 
должна быть гораздо больше центробежного потенциала, связанного со всеми возможными значениями относительных орбитальных моментов первичных фрагментов деления:
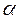(1.25)
Выполнение данного условия приводит к независимости делительных фаз от величины . Во-вторых, кинетическая энергия должна быть гораздо больше вращательных энергий первичных фрагментов деления для всех возможных значений спинов 
фрагментов
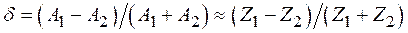(1.26)
где 
– момент инерции 
-го фрагмента. Это условие позволяет считать потенциальные делительные фазы не зависящими от спинов и суммарного спина 
первичных фрагментов деления. Наконец, время формирования угловых распределений первичных фрагментов деления 
должно быть гораздо меньше периодов вращения 
первичных фрагментов деления для всех возможных значений спинов указанных фрагментов
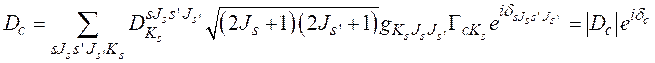(1.27)
где 
– область формирования угловых распределений первичных фрагментов деления, которые определяют угловые распределения конечных фрагментов деления. Это условие позволяет считать, что во всей области формирования угловых распределений первичных фрагментов деления оси симметрии первичных фрагментов деления совпадают по направлению с осью симметрии делящегося ядра, когда 
. Условия (1.25)–(1.27) реализуются для деления актинидных ядер при 
МэВ, 
, 
фм, 
фм и максимальных значениях и 
равных 30 и 15 соответственно. Независимость делительных фаз от , 
, 
, приводит к интерференции состояний фрагментов деления с различными квантовыми числами , , , в амплитудах УРФ деления с фиксированными квантовыми числами 
. Этот результат отличается от представлений работы , где пренебрегается интерференцией различных значений .
Как отмечалось выше, нормированное на единицу УРФ двойного деления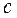 
из состояния 
традиционно рассчитывается при использовании формулы (1.6), которая имеет универсальный характер для всех каналов деления 
. В основе этой формулы лежит качественное физическое допущение, согласно которому фрагменты деления вылетают только по направлению или против направления оси симметрии 
делящегося ядра. Это означает, что УРФ деления во в.с. имеет -образный характер вида 
, где 
– угол между вектором и осью симметрии делящегося ядра , а 
. Указанные -функции можно представить как
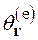(1.28)
где величина 
рассматривается в пределе 
. Формула (1.28) отражает квантовомеханическое соотношение неопределенности между орбитальным моментом и углом вылета частицы 
, из которого следует, что задание точного направления вылета частицы возможно лишь при полной неопределенности в значениях орбитального момента частицы (
). Поскольку в процессе деления ядер могут появиться только конечные значения спинов и относительных орбитальных моментов фрагментов деления, то формула (1.6) может иметь лишь приближенный характер. В то же время формула (1.6) успешно описывает широкий класс явлений, связанных с делением ядер, что свидетельствует о ее достаточно высокой точности. Понять этот результат можно, если вместо (1.28) для описания УРФ во в.с. использовать размазанные -функции вида 
:
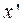(1.29)
где принимает конечные значения,
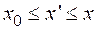(1.30)
причем фактор 
учитывает закон сохранения четности, 
– функция Хевисайда, а 
– нормировочная константа, равная
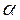(1.31)
Функция соответствует УРФ, отличным от нуля внутри конуса с осью, направленной вдоль оси и раствором угла 
при вершине конуса 
. Для приближенной справедливости формулы (1.28) необходимо, чтобы величина была достаточно мала, что означает появление больших значений максимального относительного орбитального момента в формуле (1.29).
При учете конечных значений формула (1.6) для нормированного на единицу УРФ деления (1.6) преобразуется к виду:
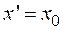(1.32)
Естественно, что формула (1.32) переходит в формулу (1.6) при .
Для последовательного получения формулы (1.32) каналовая функция 
(1.14) в л.с. преобразуется во в.с. при учете, что оси симметрии фрагментов совпадают с осью симметрии делящегося ядра, и при использовании преобразования Вигнера . С применением полученных каналовых функций во в.с. амплитуда парциальной делительной ширины выражается через произведения коэффициентов Клебша-Гордана на интеграл перекрытия 
внутренней волновой функции делящегося ядра 
с внутренними волновыми функциями фрагментов деления 
и радиальными формфакторами . Тогда зависимость амплитуды делительной ширины от относительного орбитального момента фрагментов деления определяется интегралом 
, где сферическая функция 
входит в определение каналовой функции во в.с. Используя приближение, что для всех каналов деления УРФ деления во в.с. имеют универсальный характер, приближенно описываемый размазанной -функцией (1.29) величину 
можно представить в виде 
. Подставляя полученное выражение для амплитуды в формулу (1.22) и проводя суммирование по ,,, при учете интерференции делительных амплитуд с различными ,,, и независимости делительных фаз от указанных квантовых чисел, можно представить асимптотику волновой функции , определяемую асимптотикой волновой функции 
(1.22) моды деления , как
(1.33)
где амплитуда парциальной делительной ширины 
. Используя функцию (1.33) для определения многочастичной плотности потока фрагментов деления 
в направлении радиуса-вектора в л.с. и производя интегрирование этой плотности потока по углам Эйлера 
и по внутренним координатам 
, 
фрагментов деления с учетом ортонормированности внутренних функций 
и 
, можно получить одночастичную плотность потока фрагментов 
в направлении радиуса-вектора в л.с. :
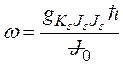(1.34)
В этом случае полное число легких и тяжелых фрагментов деления, регистрируемое в единицу времени детекторами, заполняющими 
-сферу, в канале , будет определяться интегралом от по 
и равно, как и следовало ожидать, 
, где 
– делительная ширина родительского ядра в канале . Из формулы (1.34) следует, что нормированное на единицу УРФ деления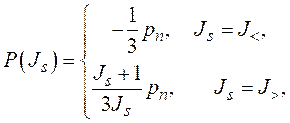 
в л.с. выражается формулой (1.32).
Поможем написать любую работу на аналогичную тему