Линейная регрессия находит широкое применение в экономике в виде четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида:
![]() = a + bx.
= a + bx.
Это уравнение позволяет по заданным значениям фактора х иметь теоретическое значение результативного признака, подставляя в него фактическое значение фактора х.
Коэффициент b является коэффициентом регрессии и характеризует наклон прямой к основной оси Ох. Обозначим через γ угол, который прямая регрессии образует с осью Ох. Имеем b= tg γ. b – является мерой зависимости y от х или мерой влияния х на y. Знак при b определяет направление регрессии. Положительная линия регрессии при положительном коэффициенте регрессии с увеличением значений х увеличивает значение y. Отрицательный коэффициент регрессии свидетельствует об отрицательной регрессии, когда с увеличением х значение y убывает.
Построение линейной регрессии сводится к оценке ее параметров а и b. Оценки параметров линейной регрессии могут быть найдены различными методами. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов. Он позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетного теоретического ![]() минимально, т.е.
минимально, т.е. ![]() . Из всего множества минимальная линейная регрессия на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией было минимальным.
. Из всего множества минимальная линейная регрессия на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией было минимальным.
Система нормальных уравнений дает возможность оценки параметров а и b.
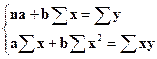
Решая эту систему уравнений либо методом последовательного исключения переменных, либо методом определителей находят искомые оценки параметров а и b.
b – коэффициент регрессии, его величина показывает среднее изменение результата при изменении фактора на единицу. Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.
Формально значение а – это значение y при х0. Если фактор х не имеет нулевого значения, то такая трактовка свободного члена а не имеет смысла. Параметр а может не иметь экономического содержания. Интерпретировать можно лишь знак при а. Если а >0, то относительное изменение результата происходит медленнее, чем изменение фактора.
Уровень регрессии всегда дополняется показателем тесной связки. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции.
![]()
Линейный коэффициент корреляции находится в границах от –1 до +1. Если b>0, то 0 ≤ r ≤ 1. Если b<0, то -1 ≤ r ≤ 0.
Величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции нулю еще не означает отсутствие связи между признаками. При иной спецификации модели связь между признаками может оказаться достаточно тесной.
Для оценки качества подбора линейной функции рассматривается квадрат линейного коэффициента корреляции, называемый коэффициентом детерминации результативного признака y, объясняемой регрессией и соответствующая величина 1- r2 – характеризует долю дисперсии y, вызванную влиянием остальных, неучтенных факторов.
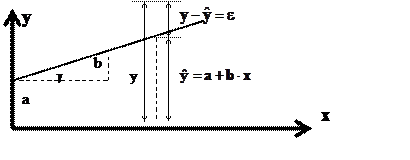 |
Поможем написать любую работу на аналогичную тему

