Два класса нелинейных регрессий.

Если между экономическими явлениями существует нелинейные соотношения, то они выражаются с помощью соответствующей нелинейной функции. Различают два класса нелинейных регрессий. Нелинейные относительно включенных в анализ объясняющих переменных, нелинейных по оцениваемым параметрам и регрессии, нелинейные по оцениваемым параметрам.

Примерами нелинейной регрессии по включенным в нее объясняющим переменным могут служить следующие функции.

• Полиномы различных степеней - y = a + bx + cx2, y = a + bx + cx2 + dx3,
• Равносторонняя гипербола - y = a + b

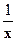
К нелинейным регрессиям по оцениваемым параметрам относятся функции

• Степенная               - y = axb.
• Показательная        - y = abx.
• Экспоненциальная – y = ea+bx.

Нелинейная регрессия, по включенным переменным, не таит каких – либо сложностей в оценке и параметров. Она определяется, как и в линейной регрессии, и методом наименьших квадратов, т.к. отмеченные функции линейны по параметрам. Для удобства оценивания параметров, эти функции можно представить в виде линейной множественной регрессии. Для этого в полиноме m – ой степени следует сделать следующие замены.

x = x1,  x2 = x2,  x3 = x3                   a = a*,  b = b*,  c = c*,  d = d*.

 = a* + b* x1 + c* x2 + d* x3.

Полином любого порядка сводится к линейной регрессии и её методам оценки параметров и проверки гипотез. Чаще всего среди полиномов используется парабола второго порядка. Нахождение ее параметров возможно методом определителей. Для равносторонней гиперболы y=a + b производим замену  = z, получается линейное уравнение регрессии y =a+bz, оценка параметров которого может быть дана методом наименьших квадратов. Регрессии нелинейные по оцениваемым параметрам подразделяют на два типа: нелинейные модели, внутренне линейные, и нелинейные модели, внутренне не линейные.

Если нелинейная модель внутренне линейна, то она с помощью преобразования может быть приведена к линейному виду.

Если нелинейная модель внутренне не линейна, то она не может быть сведена к линейной функции.

Для экономических расчетов наибольший интерес представляют внутренне линейные функции. К примеру, степенная функция путем логарифмов приводится к линейному виду

y = axb.                      →           ln y = ln a + b ln x

Соответствующие оценки параметров а и b могут быть найдены методом наименьших квадратов.

Обратная модель

Обращая обе части равенства получим линейную форму модели для переменной

При использовании линеаризуемых функций не следует проверять наличие предпосылок МНК, чтобы они не нарушили при проведении преобразований. Уравнение регрессии, так же как линейные зависимости, дополняются коэффициентом корреляции.

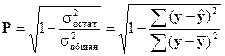
Величина данного показателя находится в границах от 0 до 1. Чем ближе к 1, тем теснее связь рассматриваемых признаков, тем более надежно каждое уравнение регрессии.