Другой вид уравнений множественной регрессии – уравнение в стандартном …….. рованном масштабе. Оценки влияния каждого фактора – признака, включенного в уравнение регрессии, на результативный признак может быть затруднена, если фактор – признаки различаются по своей сущности и имеют различные единицы измерения. В этом случае для более точной оценки влияния факторов используются множественные модели регрессии в стандартном рованном масштабе.
ty = β1t1x1 + β2t2x2 + ….. + βntnxn
![]() ,
, ![]() ,…………..
,…………..![]()
ty и tx – являются стандартизированными переменными,
β – стандартный, линейный коэффициент регрессии.
К уравнению регрессии в стандартном масштабе применим метод наименьших квадратов. Связь коэффициентов в множественной регрессии b со стандартными коэффициентами β описывается соотношением
![]()
Параметр а определяется из соотношения
a = ![]() - b1x1
- b2x2 - …. - bnxn,
- b1x1
- b2x2 - …. - bnxn,
4. Вычисление коэффициента эластичности, корреляции и детерминации.
Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле
![]()
Тесноту совместного влияния фактора на результат оценивают коэффициент или индекс корреляции, который рассчитывается
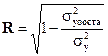
Значение индекса множественной корреляции лежит в пределах от 0 до 1. Индекс множественной корреляции в стандартном масштабе равен
![]()
Качество построения модели в целом оценивает коэффициент или индекс детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции.
Значимость уравнения множественной регрессии в целом оценивается с помощью F – критерия Фишера. Оценка значимости коэффициентов чистой регрессии производится с помощью t - критерия Стьюдента.
Поможем написать любую работу на аналогичную тему

