Оценка параметров модели с помощью МНК. Отбор факторов

При построении модели множественной регрессии возникает необходимость оценки

(вычисления) коэффициентов линейной функции, которые в матричной форме записи обозначены вектором A. Формулу для вычисления параметров регрессионного уравнения методом наименьших квадратов (МНК) по данным наблюдений приведём без вывода:

 .                                                             (3.6)

При m = 1 соотношение (3.6) принимает вид (2.5). Нахождение параметров с помощью соотношения (3.6) возможно лишь тогда, когда между различными столбцами и различными строками матрицы исходных данных X отсутствует строгая линейная зависимость (иначе не существует обратная матрица). Это условие не выполняется, если существует линейная или близкая к ней связь между результатами двух различных наблюдений, или же если такая связь существует между двумя различными факторными переменными. Линейная или близкая к ней связь между факторами называется мультиколлениарностью. Чтобы избавиться от мультиколлениарности, в модель включают один из линейно связанных между собой факторов, причём тот, который в большей степени связан с исследуемой переменной.

            На практике чтобы избавиться от мультиколлениарности мы будем проверять для каждой пары факторных переменных выполнение следующих условий:

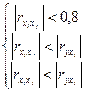   .                                                           (3.7)

То есть коэффициент корреляции между двумя факторными переменными должен быть меньше 0,8 и, одновременно, меньше коэффициентов корреляции между исследуемой переменной и каждой из этих двух факторных переменных. Если хотя бы одно из условий (3.7) не выполняется, то в модель включают только один из этих двух факторов, а именно, тот, у которого модуль коэффициента корреляции с Y больше.

            Пример. Будем считать, что торговое предприятие из Примера 1 находится в г. Барнауле, x1 – температура воздуха в г. Барнауле. Дополним данные наблюдений значениями факторной переменной x3 – значениями температуры воздуха в г. Новосибирске в период наблюдений:

Таблица 6                 

Проверим наличие мультиколлениарности между факторными переменными, произведём отбор факторов и найдём параметры линейной модели множественной регрессии. Для нахождения коэффициентов парной корреляции можно воспользоваться формулой (2.1). Поскольку вычисления будут достаточно громоздкими,

эффективнее использовать средства табличного процессора Microsoft Excel. Применив к данным из Таблицы 6 обработку Сервис/ Анализ данных/ Корреляция, получим набор коэффициентов парной корреляции:

Проверим выполнение условий (3.7) для каждой пары факторных переменных.

Для x1, x2:

- выполняется,

 - выполняется,

 - выполняется.

Все три условия (3.7) выполняются, значит мультиколлениарность между факторными переменными x1 (температура воздуха в г. Барнауле) и x2 (размер торговой наценки) отсутствует, то есть они могут использоваться в модели одновременно.

Для x1, x3:

- не выполняется,

 - не выполняется,

 - не выполняется.

Ни одно из условий не выполняется, следовательно, факторы x1 (температура воздуха в г. Барнауле) и x3 (температура воздуха в г. Новосибирске) мультиколлениарны, то есть не рекомендуется использовать их в модели одновременно. Поскольку , то фактор x1 теснее связан с исследуемой переменной y (объём продаж), чем фактор x3. Поэтому исключить из рассмотрения следует фактор x3.

Для x2, x3:

- выполняется,

 -  выполняется,

 -  выполняется.

Все три условия выполняются, значит мультиколлениарность между факторными переменными x2 и x3 отсутствует, и они могут использоваться в модели одновременно.

            Можно резюмировать, что в модели можно оставить либо пару факторов x1, x2, либо пару x3, x2. То есть выбор необходимо сделать между факторами x1 и x3. Как уже отмечалось выше, фактор x1 имеет преимущество, поскольку теснее, чем x3, связан с y. Поэтому модель для объёма продаж y мы будем строить с учётом влияния факторов x1 и x2:

.

            Для вычисления параметров модели по данным наблюдений выпишем вектор Yв и матрицу Xв:

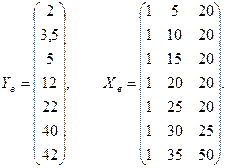
            Опуская операции транспонирования матрицы, перемножения матриц и нахождения обратной матрицы (можно воспользоваться в Excel функциями ТРАНСП, МУМНОЖ, МОБР), запишем промежуточный результат вычислений, необходимых для нахождения вектора параметров модели А по формуле (3.6):

.

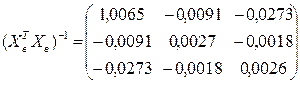Продолжая операции с матрицами в соответствии с (3.6), получим искомый вектор параметров модели:

.

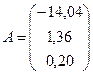То есть мы получили уравнение линейной регрессии следующего вида:

.                                       (3.8)

Значения параметров модели указывают, что в среднем при увеличении температуры воздуха в г. Барнауле на 1 градус объём продаж на изучаемом предприятии увеличивается на 1,36 единицы, а при увеличении торговой наценки на 1% объём продаж увеличивается на 0,20 единицы. Последний вывод выглядит некорректно, поскольку в реальном процессе, наоборот, увеличение наценки сдерживает рост объёма продаж.

            Определим по (3.8) расчётные значения исследуемой переменной для набора значений факторов, полученных в наблюдениях (Таблица 6), и составим ряд отклонений εi фактических значений объёма продаж от расчётных значений.  

Таблица 7