Значимость параметров модели множественной регрессии aj проверяется с помощью t-критерия Стьюдента аналогично тому, как мы проверяли значимость коэффициентов модели парной регрессии. Для каждого параметра уравнения вычисляется t-статистика:
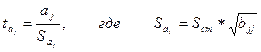. (3.9)
Здесь Sст – стандартная ошибка оценки, задаваемая соотношением (2.6), bjj – диагональный элемент матрицы 
.
Далее по таблицам (или в Excel с помощью функции СТЬЮДРАСПОБР) определяется значение tкр в зависимости от уровня значимости α и параметра n-m-1. Наконец, каждая из t-статистик (3.9) сравнивается с табличным значением. Если ׀taj׀ > tкр, то коэффициент aj считается значимым. В противном случае коэффициент не является значимым и его можно положить равным нулю, тем самым исключить из модели фактор xj (качество модели при этом не ухудшится).
Проверим значимость коэффициентов полученного нами уравнения регрессии (3.8). Вычислим стандартную ошибку оценки:
.
Тогда
.
Находим табличное значение 
. Для коэффициентов a0, a1 вычисленные t-статистики по модулю больше критического значения. Следовательно, с вероятностью 90% мы можем утверждать, что коэффициенты a0, a1 уравнения регрессии (3.8) являются значимыми.
,
следовательно, коэффициент a2 не является значимым, то есть его можно положить равным нулю, тем самым, исключив фактор x2 из рассмотрения.
Поможем написать любую работу на аналогичную тему