Применение обработки РЕГРЕССИЯ  для определения параметров модели множественной линейной регрессии и её исследования

Построение и исследование модели множественной линейной регрессии является достаточно трудоёмкой процедурой. Трудоёмкость вычислений можно существенно снизить с помощью применения в MS Excel обработки Сервис/Анализ данных/РЕГРЕССИЯ.

Рассмотрим возможности использования обработки РЕГРЕССИЯ на данных примера из п.3.2. Данные для факторной переменной x3 мы использовать не будем, поскольку x3 была удалена из рассмотрения в результате проверки факторных переменных на мультиколлениарность. После вызова обработки РЕГРЕССИЯ зададим в соответствующих окнах диапазон ячеек, в которых находятся данные для Y вместе с заголовком столбца, диапазон ячеек, в которых находятся данные для факторных переменных x1, x2 также с заголовками столбцов, поставим флажок Метки (указывает, что в первой строке диапазонов стоят названия столбцов), зададим начальную ячейку для выходного интервала, поставим флажок Остатки. После выполнения обработки в ячейках, расположенных ниже и правее ячейки, указанной нами как начальная ячейка выходного интервала будут расположены результаты. Результаты обработки группируются в 4 таблицы. Если при вызове обработки мы дополнительно поставим флажок График остатков, то будут выданы графики остатков, по горизонтальной оси которых будут отложены значения одной из факторных переменных, а по вертикальной – значения ряда остатков εi. Число графиков будет совпадать с числом факторных переменных. Рассмотрим полученные результаты.

Ошибка! Ошибка связи.

Во-первых, в колонке Коэффициенты третьей таблицы возьмём значения параметров множественной модели линейной регрессии. Уравнение модели имеет вид:

.

В колонке  t–статистика этой же таблицы находятся t-статистики для коэффициентов уравнения регрессии. Если возьмём при α=0,1 критическое значение tкр(0,1; 7-2-1)=2,13, то получим, что модули первых двух параметров превышают критической значение, а модуль третьего параметра нет. Таким образом значения а0=-14,04 и а1=1,36 следует признать значимыми, а значение а2=0,2 – незначимым. Следует отметить, что для определения значимости коэффициентов не обязательно определять критическое значение t-статистики. Достаточно сравнить соответствующие значение колонки P-Значение с выбранным уровнем значимости α  и, если оно меньше чем α, то соответствующий параметр можно признать значимым. У нас получилось 0,089 < 0,1 и 0,014 < 0,1, то есть первые два параметра можно признать значимыми с вероятностью 90%, а 0,566 > 0,1, то есть третий параметр значимым не является, то есть наценку можно исключить из рассмотрения в рамках данной модели.

            В первой таблице приведено значение коэффициента детерминации R-квадрат = 0,9102. Следовательно, можно сделать вывод, что в рамках линейной модели множественной регрессии изменение объёма продаж на 91% объясняется изменением температуры воздуха и торговой наценки.

            В колонке F третьей таблицы приведено значение F-статистики Фишера равное 20,268. Для оценки значимости уравнения регрессии в целом сравним его с критическим значением Fкр(0,1; 2; 7-2-1) = 4,32. Поскольку F-статистика больше критического значения можно сделать вывод о значимости уравнения в целом. Этот же вывод можно сделать без определения критического значения Fкр путём сравнения значения из следующей колонки третьей таблицы Значимость F, равное 0,008, с выбранным уровнем значимости α = 0,1 (для возможности сделать вывод о значимости уравнения в целом это значение не должно превышать выбранный уровень значимости).

            Для определения средней ошибки аппроксимации можно воспользоваться имеющимся в четвёртой таблице рядом остатков εi (колонка Остатки). Однако, потребуются дополнительные вычисления. Указанную таблицу следует дополнить колонкой 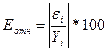, где Yi – ряд наблюдений переменной Y (в учебных задачах задан в условии) и вычислить среднее значение для этой колонке. В результате получим:

Ошибка! Ошибка связи.

Модуль вычисляется с помощью функции ABS. Мы получили E отн.ср. = 63,73%, что значительно превышает 15%, следовательно, точность модели неудовлетворительная, и её не рекомендуется использовать для прогнозирования.

            Заметим, что в первой таблице итоговых результатов имеется значение стандартной ошибки оценки, которое необходимо при построении интервального прогноза, а в последней четвёртой таблице имеется ряд расчётных значений исследуемого признака Ypi (колонка Предсказанное Y).