Проверка однородности данных

Проверка однородности данных обычно про водится на основе критерия Ирвина, который осно ван на сравнении соседних значений ряда. В соответствии с ним рассчитывается характеристикаλt :

Полученные значения сравниваются затем с табличными значениями. Если эти значения  больше табличных, то наблюдения считаются аномальными. Аномальные наблюдения либо удаляются из выборки, либо (если это временной ряд) заменяются расчетными значениями (например, средним из двух соседних значений).

Корреляция – связь между процессами, отражает степень обусловленности состояния одного процесса от другого.

Например, А коррелирует с Б означает изменение в А приводят к изменениям Б, но не обязательно наоборот. Так, температура влияет на рост и развитие растения, при этом рост растения ни как не влияет на температуру.

Зависимость между двумя случайными величинами называется вероятностной (стохастической или статистической), если каждому значению одной из них соответствует определенное (условное) распределение другого.

Например, зависимость между урожайностью и количеством внесенных удобрений — вероятностная.

Основными задачами корреляционного анализа являются:

• измерение степени связи двух или более явлений;
• отбор факторов, оказывающих наиболее существенное влияние на результативный признак на основании измерения степени связности между явлениями;
• обнаружение ранее неизвестных причинных связей. Корреляция непосредственно не выявляет причинных связей между явлениями, но устанавливает численное значение этих связей и достоверность суждений об их наличии.

При проведении корреляционного анализа вся совокупность данных рассматривается как множество переменных (факторов), каждая из которых содержит n наблюдений; xik - наблюдение i переменной k; xk - среднее значение k-ой переменной; i=1,...,n.

Парная регрессия представляет собой регрессию между двумя переменными –y и x, т. е. модель вида:

,

где y – зависимая переменная (результативный признак);

x – независимая, или объясняющая, переменная (признак-фактор).

Линейная регрессия сводится к нахождению уравнения вида

.                                                                              (1.1)

Уравнение вида  позволяет по заданным значениям фактора x находить теоретические значения результативного признака, подставляя в него фактические значения фактора x.

Построение линейной регрессии сводится к оценке ее параметров – a и b. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров a и b, при которых сумма квадратов отклонений фактических значений результативного признака y от теоретических  минимальна:

                                                                               (1.2)

,                                                          (1.5)

где ,  ,  ,  .

Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Формально a – значение y при x=0. Если признак-фактор x не может иметь нулевого значения, то вышеуказанная трактовка свободного члена a не имеет смысла, т.е. параметр a может не иметь экономического содержания.

Адекватность модели – совпадение соответствующих свойств (функций / параметров / характеристик и т.п.) модели и моделируемого объекта.

Проверка модели на адекватность позволит очертить границы применимости модели, т.е. определить при каких начальных условиях, для какого типа данных, на какой срок и с какой точностью может быть использован данный конструкт.

Оценка модели на адекватность проводится по следующим критериям:

- непротиворечивость;

- чувствительность;

- реалистичность;

- работоспособность.

Непротиворечивость - проверка на логичность полученных результатов, особенно в приближенных к критическим значениям параметров. При достижении критического уровня модель должна правильно отражать изменение состояния системы.

Например, для каждой системы существует некоторое критическое значение свойства, при достижении которого система меняет свои свойства. Например, температура кипения, температура плавления, угол наклона и пр. Если при увеличении температуры, модель не отражает процесса увеличения объема вещества, изменение его свойств, то является противоречивой.

Область вариации факторов, в которых модель дает непротиворечивые результаты – есть область применимости модели.

Чувствительность - анализ степени чувствительности модели на изменение ее входных параметров.

На сколько изменится результат, получаемый на выходе системы, если незначительно изменится значение одного из параметров? Т.е. анализ вида зависимости Y(X), где Y – моделируемое свойство системы, X входной параметр дает некоторую информацию о поведении системы.

Реалистичность (точность модели) - Соответствует ли модель частным случаям, для которых определено значение входных переменных? Такая проверка необходима для доказательства реалистичности модели, как для самого исследователя, так и для руководителя (заказчика). В модель закладываются заведомо известные данные входных переменных с известным результатом. Если на выходе получаем ожидаемый результат с удовлетворяющей нас погрешностью, то модель реалистично отображает поведение системы.

Если модель возвращает результат в качественной форме (например, экспертные диагностические системы, ставящие диагноз больному), то правильность результата должен проверять эксперт-специалист предметной области. Количество ошибок в диагностике такой системы не должно быть больше чем у эксперта.

1. Точность модели

1. Абсолютная погрешность модели

2. Относительная погрешность

Вычислив среднее значение величины по фактическим данным, получаем оценку точности модели.

Правило 1. Модель считается точной, если средняя величина относительной погрешности менее 10%.

3. Дисперсия остатков (погрешности) - характеризует степень рассеяния погрешностей модели

 где m - количество параметров в модели (для однофакторной линейной зависимости m = 2).

4. Стандартная ошибка y*

Правило 2. Выбирается та модель, при которой стандартная ошибка y* минимальна.

5. Коэффициент детерминации - отражает степень приближения отклонений прогнозируемого показателя от средней величины к отклонению относительно среднего фактических значений.

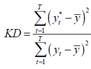
Полное совпадение тенденции - коэффициент детерминации равен 1, т.е. прогнозные (расчетные) отклонения полностью совпадут с фактическими.

Допустимое совпадение тенденции - коэффициент детерминации >=0,8.

Чем меньше коэффициент детерминации, тем хуже качество разработанной модели, ниже ее точность.

Правило 3. Выбирается та модель, при которой коэффициент детерминации не менее 0,8.

2. Реалистичность модели

Используется критерий Фишера.

Для проверки критерия вычисляется F* - фактическое значение критерия на основе модельных данных.

 Где rxy - показатель, индекс корреляции; T - объем выборки; m - количество параметров в модели.

Затем необходимо определить табличное значение Ftab = f (a,T -m) - максимально-возможное значение критерия при влиянии случайных факторов при заданном количество степеней свободы и уровне надежности (значимости) гипотезы a .

Параметр a - характеризует вероятность отвергнуть гипотезу, при том что она верна! a = 0,01; 0,05.

Правило 4! Если F* > Ftab , то гипотеза о случайности связи отклоняется и признается статистическая значимость взаимосвязи и ее надежность.

Стандартные ошибки коэффициентов модели – степень вариабельности коэффициентов модели (чем больше степень вариабельности, тем большее количество подобных трендов можно построить, используя один и тот же набор данных).

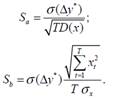
Правило 4. Выбирается такая прогнозная модель, при которой стандартные ошибки коэффициентов минимальны.

t-критерий Стюдента используется для проверки статистической гипотезы о случайной природе параметров модели, т.е. о незначимом их отличии от нуля и для оценки широты доверительного интервала модели.

Оценим реалистичность выявленной закономерности на основе анализа качества доверительного интервала.

Доверительный интервал – интервал возможных значений случайной величины, соответствующий определенному уровню доверия.

Уровень доверия (надежности) a характеризуется вероятностью того, что значение случайной величины попадет в данный интервал.

Максимальный уровень доверия – 1 или 100%.

Минимальный – 0 или 0%.

Вычисляются коэффициенты модели в рамках доверительного интервала. Если они меняют знак, то такая модель не адекватна.

(значение коэф. - Табличное значение t-критерия* Стандартные ошибки коэффициентов)

3. Работоспособность модели –

- Легко ли использовать модель на практике?

- Как быстро можно получить результат моделирования по модели?

- Не будет ли дорого стоить использование данной модели на практике? Т.е. сумма выгод от использования модели должна превышать затраты на ее создание и эксплуатацию.

Доверительный интервал оценок модели отражает интервал, в который с вероятностью надежности оценки t-критерия попадет фактическое значение. Чем шире доверительный интервал, тем «хуже» модель, т.к. в этом случае неопределенность оценки возрастает, а практическая ценность падает.

Приращение модельных оценок y* определено как:

 где tst - значение табличного t-критерия;  - СКО ошибок модели

Правило 6! Чем больше dy* относительно среднего значения, тем хуже работоспособность модели (т.е. выше разброс возможных оценок).

4. Чувствительность модели

Оценивается:

- правильностью реакции модели, т.е. соответствия знака коэффициента модели и знака корреляции;

- устойчивостью закономерности к изменению выборки данных.

Предположим, что имеется линейная модель. Удалим из выборки произвольно несколько объектов. И сравним параметры a и b этих моделей.

Модель считается устойчивой, если Da = a1 - a0 » 0 и Db = b1 - b0 » 0.

Если приращения коэффициентов удовлетворяют условию:

То найденная закономерность является приемлемо устойчивой к изменению объема выборки.

Модель, для которой выполнены все вышеперечисленные критерии будем считать адекватной.