Распределение вероятностей случайной величины

Вероятность – степень надежности свершения некоторого события, частота.

Чем чаще происходит данное событие, тем выше его вероятность.

Максимальное значение вероятности – 1, минимальное - 0.

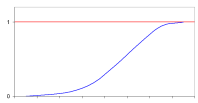
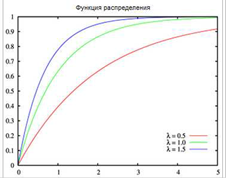
Распределение вероятностей – закономерность изменения вероятности случайной величины x : p(x < a) = F(x) .

Свойства функции распределения вероятностей:

- Функция F(x) - неубывающая.

- lim F (x) =0;

x®-¥

- lim F (x) = 1;

x®+¥

- F(x) - непрерывна слева.

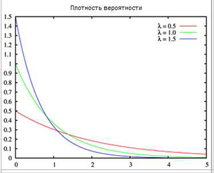
Плотность распределения вероятностей – закономерность изменения приращений вероятности распределения:

Свойства функции плотности распределения вероятностей:

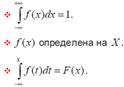
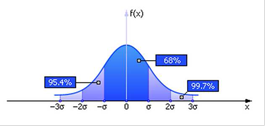
Коэффициент асимметрии – величина, характеризующая асимметрию распределения случайной величины:

 где 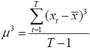 - момент третьего порядка.

- Ax > 0 - правый хвост функции плотности распределения вероятности длиннее левого (правосторонняя асимметрия);

- Ax< 0 - левый хвост функции плотности распределения вероятностей длиннее правого (левосторонняя асимметрия) .

- Ax = 0 - симметричность функции плотности распределения вероятностей относительно математического ожидания.

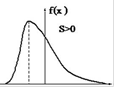
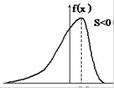
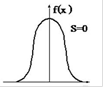
Эксцесс – мера остроты «пика» распределения вероятностей случайной величины.

 где  - момент четвертого порядка.

- Минус три в формуле принято для того, чтобы для нормально распределенной случайной величины величина gx = 0.

- gx > 0. - «острый пик», т.е. существенно большая часть наблюдений сосредоточена в области среднего значения.

- gx < 0.- «сглаженный (сплющенный) пик», т.е. чисто реализаций случайной величины на всем интервале определенности близки.

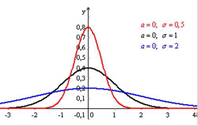
Равномерно распределенная случайная величина

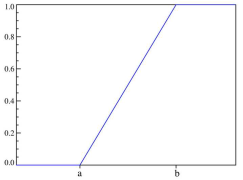
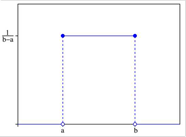
Нормально распределено случайная величина

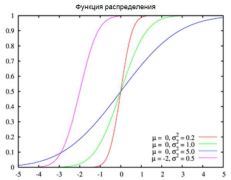
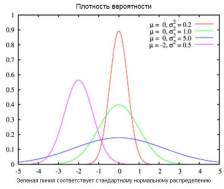
Экспоненциально распределенная случайная величина