Метод 1. Отказавшись от определения величины r статистически, можно положить r=0,5; 1 или -1.
Однако даже грубая статистическая оценка будет более эффективной, поэтому другой способ определения r с помощью статистики Дарбина-Уотсона r»1–0,5d.
Применяя затем непосредственно ОМНК, получим оценки коэффициентов.
Метод 2. Рассмотрим на примере парной регрессии:
 |
|||||
 |
|||||
 |
|||||
 |
|||||
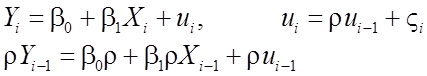(4.12)
причем 
и 
.
Ошибки в (4.12) не автокоррелированы и можно применять МНК.
Метод 3. Итеративная процедура Кохрейна-Оркатта.
а) Оценивается регрессия 
с исходными не преобразованными данными с помощью обыкновенного МНК.
б) Вычисляются остатки ei.
в) Оценивается регрессия ei=rei-1+ςi, и коэффициент при ei-1 дает оценку r.
г) С учетом полученной оценки r уравнение 
преобразовывается к виду (4.12), оценивание которого позволяет получить пересмотренные оценки коэффициентов b0 и b1.
д) Вычисляются остатки регрессии (4.12) и процесс выполняется снова, начиная с этапа в).
Итерации заканчиваются, когда абсолютные разности последовательных значений оценок коэффициентов b0, b1 и r будут меньше заданного числа (точности).
Подобная процедура оценивания порождает проблемы, касающиеся сходимости итерационного процесса и характера найденного минимума: локальный или глобальный
Метод 4. Метод Хилдрета-Лу.
Основан на тех же принципах, что и рассмотренный метод 3, но использует другой алгоритм вычислений. Здесь регрессия (4.12) оценивается МНК для каждого значения r из диапазона с некоторым шагом внутри него. Значение, которое дает минимальную стандартную ошибку для преобразованного уравнения (4.12), принимается в качестве оценки r, а коэффициенты регрессии определяются при оценивании уравнения (4.12) с использованием этого значения.
Метод 5. Метод Дарбина.
Получаем оценку ρ как коэффициента при Yi-1 в уравнении
Вычисляем значения преобразованных переменных
и применяем к ним обыкновенный МНК. Получаем искомые оценки коэффициентов регрессии.
Поможем написать любую работу на аналогичную тему