Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида: 
, где y – зависимая переменная (результативный признак); x – независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными x и y нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина y складывается из двух слагаемых:
, где y – фактическое значение результативного признака; 
– теоретическое значение результативного признака, найденное исходя из уравнения регрессии; e – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. Случайная величина e называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.
В парной регрессии выбор вида математической функции может быть осуществлен тремя методами: 1) графическим; 2) аналитическим, т.е. исходя из теории изучаемой взаимосвязи; 3) экспериментальным. Линейная регрессия имеет вид: y = a+b*x+E это уравнение позволяет по заданным значениям фактора x находить теоретические значения результативного признака, подставляя в него фактические значения фактора x . Построение линейной регрессии сводится к оценке ее параметров – a и b. Формально a
– значение y при x =0. Если признак-фактор x не может иметь нулевого значения, то вышеуказанная трактовка свободного члена a не имеет смысла, т.е. параметр a может не иметь экономического содержания. Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Готовые формулы для нахождения параметров модели: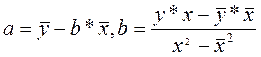 
Поможем написать любую работу на аналогичную тему